Domyślam się że chodzi o koło a nie okrąg. Więc:
Rozwiązanie O(n^2):
result = 0;
for x in [-r; r]:
for y in [-r; r]:
if inside_circle(x, y):
result++
return result;
Gdzie inside_circle to funkcja sprawdzająca czy dany punkt leży w szukanym kole (to trywialne i wynika bezpośrednio z równania koła).
Rozwiązanie O(n):
result = 0
for x in [-r; r]:
result += vertical_points(x) * 2 - 1
return result
Gdzie vertical_points(x) to funkcja mówiąca jak wiele całkowitych punktów znajduje się w kole dla danej współrzędnej x, powyżej osi OX:
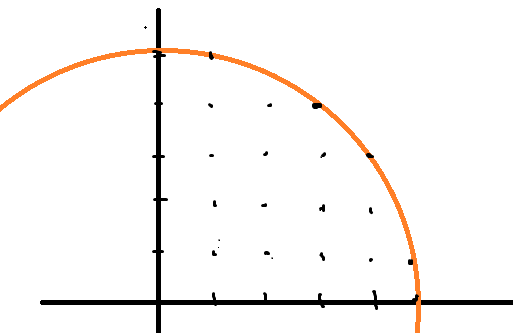
(zaawansowana ilustracja przykładowa, tutaj vertical_points(1) = 6, vertical_points(2) = 5, vertical_points(3) = 5, vertical_points(4) = 4, vertical_points(5) = 2).
Jak tą funkcję zdefiniować (bez pętli)?
x^2+y^2<=r^2
y^2<=r^2-x^2 // tylko y >= 0
y <= sqrt(r^2-x^2)
(przy czym wynikiem jest floor(y), bo bierzemy pod uwagę tylko punkty całkowite).
PS. Wszystkie przykłady dla kół o środku w (0, 0), ale bardzo prosto to uogólnić do dowolnie położonych kół.
PPS. Obie funkcje można przyśpieszyć o stałą, zauważając że wystarczy wyliczyć ilośc punktów w ćwiartce/połowie koła, i pomnożyć razy cztery/dwa. Ale komplikowało to rozwiązanie (trzeba pilnować żeby dwa razy nie policzyć jednego punktu) więc nie zostało tu zaimplementowane.
PPPS. Czy da się to zrobić w czasie lepszym niż O(n) - nie wykluczam, ale nie mam pomysłu z głowy od razu.
Może np. jakiś matematyk potrafiłby znaleźć na to bezpośredni wzór, bez żadnych petli.
