Problem ze zrozumieniem rozwiązania zadania

Mam takie zadanie:

W Bajtocji jest n miast. Miasta są połączone jednokierunkowymi drogami. Każda droga łączy tylko dwa miasta i nie przechodzi przez żadne inne. Król Bajtazar chce się dostać z pierwszego miasta do n-tego, przemieszczając się jak najmniejszą liczbą dróg. Postanowił, że w dzień jego wyprawy może zostać zmieniony kierunek jazdy niektórych dróg, jednak ze względów praktycznych liczba dróg, w których kierunek się zmieni, nie może przekroczyć k. Król musi przygotować się do podróży, więc wybór dróg do zmiany kierunku jazdy powierzył Tobie. Możesz założyć, że przy obecnych kierunkach dróg król będzie mógł dotrzeć z pierwszego miasta do miasta numer n.

Wejście Pierwszy wiersz wejścia zawiera trzy liczby całkowite n, m oraz k (2 <= n <= 10 000, 1 <= m <= 100 000, 0 <= k <= 50) oznaczające, odpowiednio, liczbę miast, liczbę dróg w Bajtocji oraz liczbę dróg, dla których można zmienić kierunek jazdy. Miasta są ponumerowane liczbami od 1 do n. W kolejnych m wierszach znajdują się po dwie liczby całkowite. W i-tym z nich są liczby ai i bi (1 <= ai , bi <= n) reprezentujące jednokierunkową drogę prowadzącą z miasta ai do miasta bi

Wyjście Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą równą minimalnej liczbie dróg, jakie Bajtazar musi przejechać, aby dostać się z miasta numer 1 do miasta numer n, z uwzględnieniem możliwości zmian kierunku jazdy maksymalnie k dróg.

Przykład

Dla danych:

5 6 1

1 2

2 3

3 4

4 5

3 1

5 2

Poprawna odpowiedź to:

2

Wyjaśnienie: Bajtazar pojedzie drogą od 1 do 2 zgodnie z kierunkiem jazdy, a następnie drogą od 2 do 5, dla której został zmieniony kierunek jazdy.

No i mam taką odpowiedź:
Zadanie możemy rozwiązać w czasie O(k · (n + m)).

• Tworzymy k kopii grafu. W ramach każdej kopii krawędzie są takie jak w oryginalnym grafie, a z wierzchołka u w kopii i do wierzchołka v w kopii i + 1 jest krawędź wtedy i tylko wtedy, gdy w oryginalnym grafie jest krawędź v → u. Na końcu znajdujemy minimalną odległość do wierzchołka docelowego w dowolnej kopii.

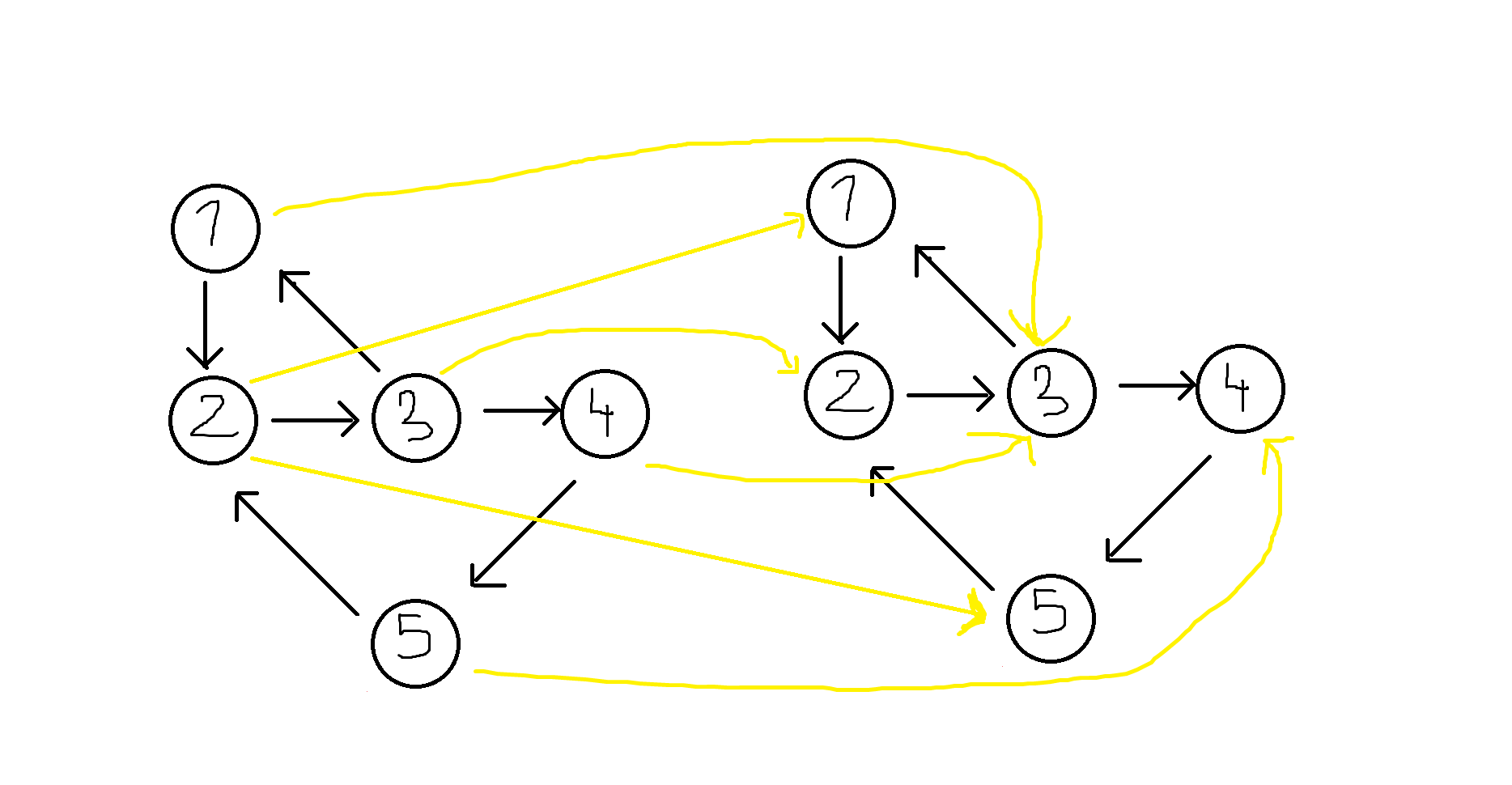
Nie rozumiem tego rozwiązania przecież robiąc k kopii dla przykładu testowego (czyli 1) otrzymalibyśmy coś takiego

Chodzi o to, że kopie grafu są połączone odwrotnością krawędzi.

Czyli (wierzchołek 2 z grafu 1) jest połączony z (wierzchołkiem 5 z grafu 2).

W takim wypadku trzeba znaleźć najkrótszą ścieżkę z (wierzchołka startowego grafu 1) do (wierzchołka docelowego dowolnego grafu od 1 do n). Możesz pomyśleć o tym, że kopie grafu utworzyły nowy graf.

tak ?

Szukasz minimalnej drogi w pierwszym grafie (z k kopii), jak widać jest to: 1->2->3->4->5, w punkcie 2 "przeskakujesz" na następnną kopię i szukasz najkrótszej drogi, tu jest 2->5, czyli w sumie 2.

Dlaczego coś takiego działa?

Bo stworzyłeś graf, który ma k możliwych zakończeń. Przejście pomiędzy wierzchołkiem z grafu i do grafu i+1 jest równoznaczne z odwróceniem drogi. Maksymalnie takich przejść można zrobić k, ponieważ masz k kopi grafu. Czyli szukając najkrótszej ścieżki z z wierzchołka startowego grafu 1 do wierzchołka końcowego grafów 1..n, odwrócisz drogę maksymalnie k razy.

Szukamy normalnym Dijkstrą zapisując "alternatywy" z małą heurystyką nie dorzucamy do stosu miasta w odległości >=(k+1)*n

#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
using namespace std;

struct edge
{
	int city,reverse;
	edge(int city,bool reverse):city(city),reverse(reverse) {}
};

struct alter
{
	int distance,reverse;
	alter(int distance=0,int reverse=0):distance(distance),reverse(reverse) {}
	bool operator==(const alter &a)const
	{ 
		return (distance==a.distance)&&(reverse==a.reverse);
	}
};
static alter empty(-1,-1);

struct node
{
	bool marked;
	vector<alter> alters;
	vector<edge> roads;
	node():marked(false) {}
};

int main()
{
	size_t nodecount,edgecount,changecount;
	cin>>nodecount>>edgecount>>changecount;
	vector<node> graph(nodecount+1);
	for(size_t from,to;(edgecount--)&&(cin>>from>>to);)
	{
		graph[from].roads.push_back(edge(to,0));
		graph[to].roads.push_back(edge(from,1));
	}
	int i=0;
	list<int> queue;
	graph[1].marked=true;
	graph[1].alters.push_back(alter());
	queue.push_back(1);
	while(!queue.empty())
	{
		int curr=queue.front();
		queue.pop_front();
		graph[curr].marked=false;
		for(const alter &a:graph[curr].alters)
		{
			int distance=a.distance;
			int reverse=a.reverse;
			for(const edge &e:graph[curr].roads)
			{
				int newreverse=reverse+e.reverse;
				if(newreverse>changecount) continue; // drobna heurystyka
				int newdistance=distance+1;
				int city=e.city;
				bool push=true;
				vector<alter> &alters=graph[city].alters;
				for(alter &v:alters)
				{
					int olddistance=v.distance;
					int oldreverse=v.reverse;
					if((olddistance<=newdistance)&&(oldreverse<=newreverse))
					{
						push=false;
						break;
					}
					else if
					(
						((olddistance>=newdistance)&&(oldreverse>newreverse))
						||
						((olddistance>newdistance)&&(oldreverse>=newreverse))
					)
					{
						v=empty;
					}
				}
				alters.resize
				(
					remove(alters.begin(),alters.end(),empty)
					-
					alters.begin()
				);
				if(push)
				{
					graph[city].alters.push_back(alter(newdistance,newreverse));
					if(!graph[city].marked)
					{
						graph[city].marked=true;
						queue.push_back(city);
					}
				}
			}
		}
	}
	int distance=nodecount;
	for(alter &v:graph[nodecount].alters)
	{
		if(distance>v.distance) distance=v.distance;
	}
	cout<<distance;
	return 0;
}