O co chodzi z problem P != NP

O co chodzi z tym problem, bo wydaje mi się że rozumiem ale nie jestem pewien. Napisze co mi się wydaje. P oznacza algorytm o z łożonośći wielomianowej. NP oznacza algorytm o złozności nie wielomianowej. Problem NP != P lub NP == P polaga na tym żebby udowodnić ze da się zaminić każdy algorytm a algorytm o złożoności obliczeniowej wielomianowej lub nie da sie zamienić chociaż jednego?
Wydaje mi sie że to zbyt prosty problem w takiej formie, naprawde tak jest? czego nie zrozumiałem lub pominąłem?

ed. Doczytałem trochę i problem NP to taki którego podzbiór można sprawdzić w czasie wielomianowym, ale sam problem ma lub nie ma wiekszą złożoność. Tylko ciągle wydaje mi się to za prostę.Co robie zle?

_flamingAccount napisał(a):

Wydaje mi sie że to zbyt prosty problem w takiej formie, naprawde tak jest? czego nie zrozumiałem lub pominąłem?

Jeśli jest prosty, to spróbuj sam udowodnić ;)

Jeżeli próbujesz wziąć się za P = NP, musiałbyś udowodnić, że każdy problem NP jest P, lub że nie może istnieć problem NP który nie byłby P. Dla P != NP musiałbyś być w stanie udowodnić, że istnieje przynajmniej jeden problem NP, który nie może być P. Przy czym dowód nie może polegać na tym, że główkowałeś przez 50 lat i nic nie wymyśliłeś :P

Problem jest łatwy do zrozumienia, ale trudny do udowodnienia. Polecam poczytać o SAT. Nagroda za udowodnienie tego lub owego to milion dolarów i już kolejne pokolenie informatyków i matematyków nad tym ślęczy bez powodzenia.

Prowokacyjnie odpowiem że wydaje mi się to zbyt prostę(pewnie za 3 dni dojdzie do mnie że się ośmieszam, na razie jestem pewny swego). To czego nie jestem pewien, to jaka jest definicja problemu np, jak sprawdzić udowodnić że coś jest NP. Wybrać zły problem to jest najprostszy bład jaki można popełnić. Czy wystarczy zeby problem(tj jego podzbiór) był weryfikowalny w czasie wielomianowym zeby był klasy np?

Tak, wystarczy, że dowolny problem z klasy NP zakodzisz ze złożonością wielomianową i dowód masz. Aczkolwiek wszystko wskazuje, że jest inaczej. I tu pojawiają się schody, bo wtedy trzeba udowodnić, że czegoś nie da się zrobić ze złożonością wielomianową.

@tsz to co piszesz jest prostą cześcią. Założmy ze chce wymyślić nowy problem na potrzeby dowodu, jak udowodnić/sprawdzić ze ten problem jest rzeczywiści klasy NP?
Czy sam brak rozwiązania innego niż wielomianowe, przy róznoczesnej możliwości zweryfikowania go wielomianowo wystarczy?

Z tego, co pamiętam ze studiów to każdy problem NP da się sprowdzić do problemu SAT, nawet jeśli tego nie widać na pierwszy rzut oka.

wpadłem na to co napisałeś dosłownie 4s sekundy przed powiadomieniem tylko pomyślałem o innym problemie. Jeśli można sprowadzić problem dowodowy w czasie wielomianowym do do dowolnego problemu NP. to w takim wypadku problem dowodowy problem jest problemem np.

Masz rację. Dowolny problem można skomplikować bardziej niż to potrzebne :D

wariant problem 4 kolorow jest taki, ze istnieja grafy planarne ktore mozna pokoloryzowac min 3 kolorami, a moze nawet 2. Wiec mozna sobie zadac pytanie: jaki jest min liczba kolorow jaka mozna kolororowac dany graf planarny. Wiec wiemy ze mozna na pewno pokolorowac 4, ale czy mozna 3? Nie da sie powiedziec bez sprawdzenia. Mozna pokolorowac 3, ale czy mozna 2? Nie da sie stwierdzic bez sprawdzenia. Za problemy typu NP rozumiem takie, gdzie nie ma innego rozwiazania problemu niz sprawdzenie wszystkich kombinacji/permutacji.

lambdadziara napisał(a):

Za problemy typu NP rozumiem takie, gdzie nie ma innego rozwiazania problemu niz sprawdzenie wszystkich kombinacji/permutacji.

Bzdura. Dyskretny problem plecakowy jest NP, a rozwiązuje go programowanie dynamiczne.

O co chodzi z tym problem, bo wydaje mi się że rozumiem ale nie jestem pewien. Napisze co mi się wydaje. P oznacza algorytm o z łożonośći wielomianowej. NP oznacza algorytm o złozności nie wielomianowej.

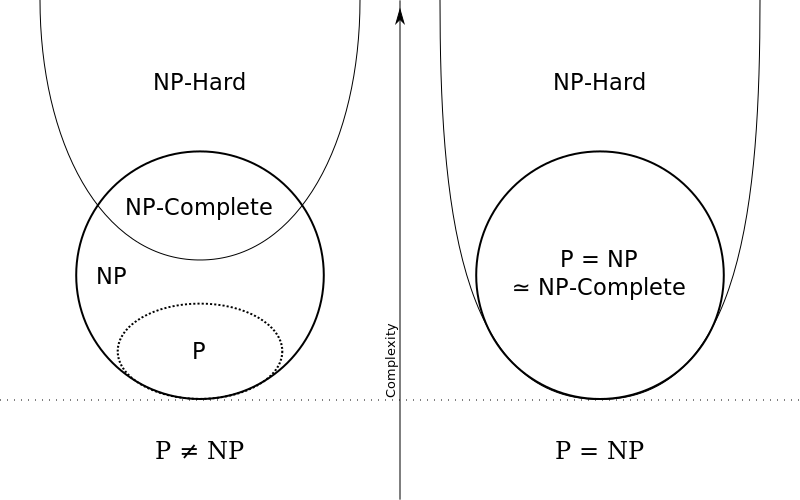
Nie. P zawiera się w NP, więc problemy z rozwiązaniami o złożoności wielomianowej zawierają się zarówno w P jak i NP. Inaczej mówiąc, NP jest nadzbiorem P i to wynika wprost z definicji. Problem polega na tym czy istnieją problemy należące do NP, ale nie należące do P.

ed. Doczytałem trochę i problem NP to taki którego podzbiór można sprawdzić w czasie wielomianowym, ale sam problem ma lub nie ma wiekszą złożoność. Tylko ciągle wydaje mi się to za prostę.Co robie zle?

Wiki mówi tak:

Problem NP (ang. nondeterministic polynomial, niedeterministycznie wielomianowy) – problem decyzyjny, dla którego rozwiązanie można zweryfikować w czasie wielomianowym. Równoważna definicja mówi, że problem jest w klasie NP, jeśli może być rozwiązany w wielomianowym czasie na niedeterministycznej maszynie Turinga.

A więc mamy:

• problem typu P może być rozwiązany w czasie wielomianowym na deterministycznej maszynie Turinga (a co za tym idzie także na niedeterministycznej maszynie Turinga)
• problem typu NP może być rozwiązany w czasie wielomianowym na niedeterministycznej maszynie Turinga

Różnica między deterministyczna, a niedeterministyczną maszyną Turinga jest opisana na Wiki, ale może podam przykład. Weźmy na tapet https://pl.wikipedia.org/wiki/Problem_sumy_podzbioru Rozwiązanie (na potrzeby rozważań) może być takie:

bool sumsToZero(int[] numbers) {
  return sumsToZero(numbers, 0, false, 0);
}

bool sumsToZero(int[] numbers, int index, bool nonEmpty, int cumulativeSum) {
  if (index == numbers.length) {
    return nonEmpty && cumulativeSum == 0;
  }
  return spawn(() => sumsToZero(numbers, index + 1, nonEmpty, cumulativeSum)) ||
    spawn(() => sumsToZero(numbers, index + 1, true, cumulativeSum + numbers[index]));
}

Przy założeniu, że mamy jeden wątek to powyższe rozwiązanie ma złożoność O(2^n) (czyli niewielomianową). Jednak gdy założymy, że mamy dostępną nieskończoną liczbę wątków to powyższe rozwiązanie ma złożoność O(n) (czyli wielomianową). Na tym mniej więcej polega różnica między deterministycznymi a niedeterministycznymi maszynami. W niedeterministycznej maszynie rozwiązującej problem w czasie wielomianowym:

• startujesz z jednym wątkiem (tak jak w deterministycznej maszynie)
• stworzenie dodatkowego wątku zabiera czas O(1) w wątku tworzącym
• dostępnych wątków jest nieskończona ilość (w "praktyce" jest skończona, bo skoro stworzenie nowego wątku zabiera czas, a startujesz z jednym to nie stworzysz nieskończonej liczby wątków w skończonym czasie)
• każdy wątek ma swoją osobną maszynę/ rdzeń/ obojętne, chodzi o to, że stworzenie nowych wątków nie spowalnia wykonywania żadnego z nich
• czas wykonywania każdego z wątków jest wielomianowy (tak jak w deterministycznej maszynie, gdzie jest tylko jeden wątek)

tsz napisał(a):

Masz rację. Dowolny problem można skomplikować bardziej niż to potrzebne :D

:D Tak, ale ja próbowałem redukować się do problemu który jest udowodniony jako P, może stąd wydawało mi się to wszystko zaproste.

@lambdadziara

Za problemy typu NP rozumiem takie, gdzie nie ma innego rozwiazania problemu niz sprawdzenie wszystkich kombinacji/permutacji.

Cała sztuka polega na tym żeby udowodnić właśnie że tak jest, bo to nie jest pewne.

@Wibowit

Nie. P zawiera się w NP, więc problemy z rozwiązaniami o złożoności wielomianowej zawierają się zarówno w P jak i NP. Inaczej mówiąc, NP jest nadzbiorem P i to wynika wprost z definicji

Znasz jakąś dobrą definicje, bo trafiłem na problem wiem że nic nie wiem a internet, jest na tyle kiepski źródłem informacji że nie dokońca ufam w w to co czytam. Tzn. podałeś definicje z wikipedi i to się ceni, ale sam z powodu braku podstaw bałem sie jej. Czyli jeśli znajdę problem którego wynik można w czasię wielomianowym, sprawdzić dla konkretnego przypadku, oraz problem można rozwiązać w czasie wielomianowym mając nie skończenie wiele rdzeni, to mogę bezpiecznie zakładać że problem jest klasy NP. Bez redukcji go do znanego problemy klasy NP. Dobrze rozumuję?

I idąc dalej, jeśli znajdę jeden problem o właściwościach opisanym wyżej którego nie da sie w czasię wielomianowym zredukować do problemu o złożności wielomianowej to udownie że NP != P?

Czyli jeśli znajdę problem którego wynik można w czasię wielomianowym, sprawdzić dla konkretnego przypadku, oraz problem można rozwiązać w czasie wielomianowym mając nie skończenie wiele rdzeni, to mogę bezpiecznie zakładać że problem jest klasy NP. Bez redukcji go do znanego problemy klasy NP. Dobrze rozumuję?

Żeby problem był klasy NP to wystarczy, że sprawdzenie wyniku da się zrobić w czasie wielomianowym. Do problemów klasy NP należą zarówno:

• problemy klasy P (czyli np sortowanie bąbelkowe jest klasy NP, bo poprawność wyniku możesz sprawdzić w czasie wielomianowym)
• problemy klasy NP
• problemy NP-zupełne

Diagram Eulera z Wikipedii naprawdę nie jest trudny do ogarnięcia:

W obu przypadkach (zarówno przy P = NP jak i P != NP) widać, że:

• P zawiera się całkowicie w NP, a więc dowolny problem klasy P jest też klasy NP
• NP-complete zawiera się całkowicie w NP, a więc dowolny problem NP-zupełny jest też klasy NP
• NP-complete zawiera się całkowicie w NP-hard, a więc dowolny problem NP-zupełny jest też NP-trudny (ale NP-trudnymi się w tym wątku nie zajmujemy)

Jeszcze innymi słowy:

• jeżeli mówimy, że problem jest klasy NP to nie wykluczamy, że jest klasy P (bo P zawiera się w NP)
• jeżeli mówimy, że problem jest klasy P to z definicji jest też klasy NP (jeśli ktoś tego nie widzi nawet na diagramach Eulera to już nie wiem co może pomóc)

Co więcej: jeśli ktoś udowodni, że P = NP to podział problemów na problemy klasy P i klasy NP straci sens, bo przecież obie kategorie będą oznaczać dokładnie to samo.

Wracając jeszcze do:

Bez redukcji go do znanego problemy klasy NP. Dobrze rozumuję?

Te redukcje odnoszą się do problemów NP-zupełnych. Z diagramu Eulera dla przypadku P != NP wynika, że dopuszczalne jest istnienie problemu (w sensie nie wiadomo czy istnieje, ale jeśli istnieje to nie psuje całej teorii) klasy NP, który jednocześnie nie jest NP-zupełny i nie jest klasy P. Z tego wynika, że dowodząc, że problem X będący klasy NP nie jest klasy P nie musisz w ogóle sprawdzać, czy problem X jest NP-zupełny.

Inaczej rzecz biorąc:

• jeśli chcesz dowieść, że P != NP to wystarczy dla dowolnego wybranego problemu klasy NP udowodnić, że nie jest klasy P (bo wystarczy jeden kontrprzykład, by obalić tezę)
• jeśli chcesz dowieść, że P = NP to wystarczy dla dowolnego wybranego problemu NP-zupełnego udowodnić, że jest klasy P (bo każdy problem klasy NP można zredukować w czasie wielomianowym do problemu NP-zupełnego, więc załatwiając jeden problem NP-zupełny załatwiamy wszystkie problemy klasy NP)

A i pamiętaj, że nie musisz tego udowadniać. Możesz pokazać, że teoria jest nieprawdziwa, lub nierozwiązywalna i to też będzie niejako rozwiązaniem problemu.

Wg. mnie najlepiej o tym myśleć w kategoriach maszyn Turinga. Maszyna niedeterministyczna ma dwie interpretacje:

1. Kwantowa - załóżmy że maszyna ma nieterministyczne przejścia do stanów A1 ... AN. Zakładamy że maszyna przechodzi do wszystkich stanów na raz i teraz mamy tak jakby N maszyn. Jeżeli któraś z tych maszyn znajdzie rozwiązanie to uznajemy że pierwotna maszyna znalazła rozwiązanie.
2. Wyrocznia - mamy wyrocznie która mówi które z niedeterministycznych przejść wybrać i to wybieramy.
   Za każdym razem jeżeli jesteśmy w stanie udowodnić że taka niedeterministyczna maszyna jest w stanie w czasie wielomianowym rozwiązać problem to wiemy że problem zawiera się w NP (P zawiera się w NP dla przypomnienia).

Podobną operację można wykonać z użyciem pamięci. Tam okazało się że problem NP-pamięciowy == P-pamięciowy. Stąd wiele osób na początku sądziło że z czasowym-NP będzie podobnie. Niestety wygląda na to że czasowe NP != czaswe P. No ale nikt tego jeszcze nie udowodnił pomimo 1M $ nagrody. Co więcej pojawiły się głosy sceptyków że to może jedno z tych twierdzeń co w systemie nie ma dowodu choć jest prawdziwe (aka Godel) - w mojej opinii to przesada. Niektóre problemy matematyczne czekały i po 300 lat na rozwiązanie.

OP najlepiej zrobi jak chwyci jakąś książkę o złożoności obliczeniowej. Tam nie tylko będzie wyjaśnione co to NP i P ale i inne ciekawe rzeczy się pojawią np. funkcja Ackermana.