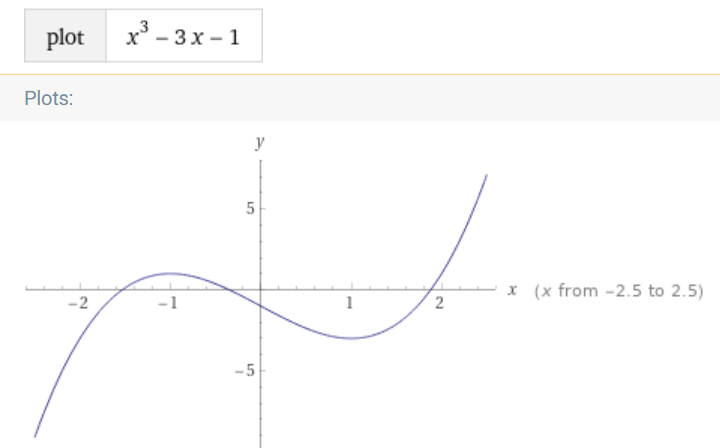
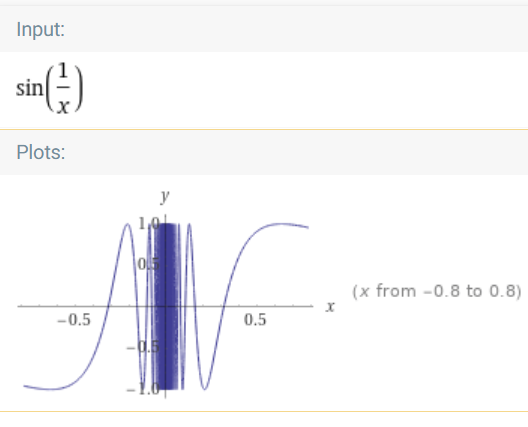
Próba uzasadnienia - dlaczego informacja całkowa podnosi rząd o 2 a nie o tylko 1?
To prawdopodobnie wynika wprost z liczby danych w interpolacji.
informacja typu: y, y', y'', ... jest jednopunktowa,
natomiast całkowa wymaga minimum 2 punktów: int_a^b fdx = F(b) - F(a); ewidentnie mamy tu dwa punkty: x=a i x=b, i stąd wzrost rzędu o 2.
Można to łatwo uzasadnić na przykładzie metody Newtona:
w każdym kroku używamy tu y(x1) i y'(x1), czyli dwóch wartości w jednym punkcie - dlatego rząd = 2.
Ale przecież można użyć stare - wcześniejsze obliczenia, z innego punktu: y(x0) i y'(x0);
i teraz w sumie mamy aż 4 parametry, zatem rząd będzie 4, nie 2!
Procedura szukania zera w zadanym przedziale [a,b] z użyciem: y i y':
daje nam informację typu: y(a), y'(a), y(b), y'(b) w każdym kroku => rząd 4 na 100%!
Całka pracuje na przedziałach, więc można to przedefiniować odpowiednio,
i w ten sposób otrzymamy metodę rzędu 4 z całką y, y i y', bo to będzie oparte na 4 parametrach tak czy siak!!! :)