nie da się zbudować koła o obwodzie wymiernym

założenie jest takie że nie da się zbudować koła o obwodzie wymiernym,

ponieważ znamy jego stosunek do średnicy który jest niewymierny, jeśli to

średnica jest niewymierna to błąd, ponieważ średnica może być dowolna

znowu założyłeś wątek bez konkretnego pytania

Zacznijmy od tego, że w ogóle w naszym świecie nie możemy zbudować perfekcyjnego koła, każde z nich zawsze będzie tylko jakimś uproszczeniem/wyrobem koło-podobnym, zatem dalsze dywagacje na ten temat nie mają sensu :P
Edit: chyba, że masz coś innego na myśli. Sam już nie wiem, w treści nie ma nawet pytania...

O = 2 * PI * r

r = 1/PI
O = 2 * PI * 1/PI
O = 2

Nie widzę problemu w zbudowaniu koła o obwodzie wymiernym. Dalszą część postu ciężko dla mnie zrozumieć (pomijam brak pytania).

Może chodzi o to, że mając dany odcinek o długości wymiernej, nie da się zbudować okręgu o obwodzie wymiernym używając tylko nieskończenie precyzyjnego cyrkla i linijki?

To nie jest tak w ogóle problem kwadratury koła? Który sprowadza się tutaj do zbudowania odcinka o niewymiernej długości.

Zacznijmy może od tego, że biorąc pod uwagę powyższe (takie detale etc.), nie da się nawet zbudować/zrobić odcinka o długości niewymiernej. Reszta jest tego konsekwencją.

@Liczba niewymierna, bzdury pleciesz. Da się.

liczba niewymierna napisał(a):

Zacznijmy może od tego, że biorąc pod uwagę powyższe (takie detale etc.), nie da się nawet zbudować/zrobić odcinka o długości niewymiernej. Reszta jest tego konsekwencją.

Bierzesz odcinek, i budujesz przy jego pomocy trójkąt równoramienny, prostokątny. Badum tss... Done.

@up jeśli nie da się dokładnie określić ile jakaś liczba wynosi (w przypadku liczb niewymiernych się nie da) to nie da się również zbudować odcinka o takiej długości - tylko przybliżoną długość.

A dowolny pierwiastek kwadratowy konstruujemy tak:

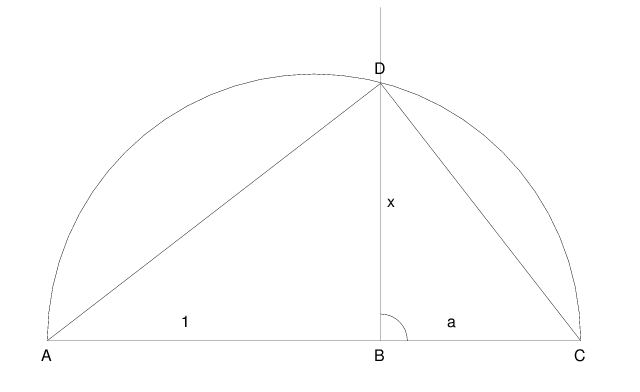
Trójkąty ABD i BCD są podobne, kąt przy wierzchołku B jest prosty. Odcinek AB ma długość 1, odcinek BC ma długość a, odcinki AB i BC leżą wzdłuż jednej prostej, odcinek AC jest średnicą półokręgu. Punkt D jest punktem przecięcia półokręgu AC i prostej prostopadłej do AC. Długość skonstruowanego odcinka BD oznaczamy przez x.

liczba niewymierna napisał(a)

jeśli nie da się dokładnie określić ile jakaś liczba wynosi (w przypadku liczb niewymiernych się nie da)

Nie da się?

dokładnie.

Hahaha...
@winerfresh no to narysuj mi odcinek o długości Pi - powodzenia! Możesz korzystać z dowolnych narzędzi - ale żeby wyszło Pi a nie jakaś Pi podobna liczba.
@TomRiddle No to możesz pomóc winerfresh-owi w tym banalnym zadaniu z "2 klasy".
@bogdans Tak, zaprezentowany przez Ciebie sposób z pewnością jest dokładny do bólu. No to możesz się dołączyć do w/w zadania.
@Azarien A możesz mi powiedzieć ile wynosi ta "liczba" nad znakiem sumy? Bo z tego co wiem to "nieskończoność" jest liczbą abstrakcyjną a to dowodzi, że ten Twój wzór również jest abstrakcyjny i nie da się go określić. A co za tym idzie nie da się dokładnie narysować prostej o długości niewymiernej.
Czy coś jeszcze pominąłem?

@liczba niewymierna, ty odróżniasz konstrukcje poprawne teoretycznie od realnie wykonywanych? Realnie to nie skonstruujesz nawet odcinka o długości 2 mając do dyspozycji odcinek o długości 1. Nawet nie masz możliwości sprawdzenia czy ten ten dany odcinek naprawdę ma długość 1.
Podsumowując, realnie nie można skonstruować niczego, a co jest teoretycznie możliwe do skonstruowania opisałem wcześniej w komentarzu.

bogdans napisał(a):

@liczba niewymierna, ty odróżniasz konstrukcje poprawne teoretycznie od realnie wykonywanych? Realnie to nie skonstruujesz nawet odcinka o długości 2 mając do dyspozycji odcinek o długości 1. Nawet nie masz możliwości sprawdzenia czy ten ten dany odcinek naprawdę ma długość 1.

Ale mi nie chodzi o to, że się nie da bo nie zrobię tego wystarczająco dokładnie tylko się nie da, ponieważ nie da się dokładnie określić ile liczba niewymierna wynosi! Możesz określić liczbę Pi do kilku miliardów cyfr po przecinku, ale nie będziesz w stanie dokładnie jej określić.

nie można skonstruować ze znaczniej głębszych powodów niż ten, że jej rozwinięcie dziesiętne jest nieskończone i nieokresowe. Przekątna kwadratu o boku 1 ma długość mimo tego, że rozwinięcie liczby jest nieskończone i nieokresowe.
Na marginesie, wykazujesz się zupełną ignorancją matematyczną. Jeżeli chcesz dalej dyskutowąć, to przestań być anonimowy.

Autor wątka ma jednak częściowo rację, że geometryczne skonstruowanie koła o obwodzie wymiernym jest niemożliwe.

Ale można by wziąć "sznurek" o wymiernej długości, i zwinąć go w okrąg. Pytanie tylko, jak?

Przychodzi mi do głowy narzucenie pętli na czubek stożka, tak aby opadła i przyjęła kształt okręgu.
Zakładamy tutaj zerową grubość sznurka, niezerową masę, jego nierozciągliwość, brak tarcia sznurka o powierzchnię stożka, brak oporu powietrza i jednorodne pole grawitacyjne.
Trudno to chyba jednak nazwać "konstrukcją"...

Myślę, że to jest w zasadzie ten sam problem co kwadratura koła, ergo da się udowodnić, że taka konstrukcja jest niewykonalna.

Ale mi nie chodzi o to, że się nie da bo nie zrobię tego wystarczająco dokładnie tylko się nie da, ponieważ nie da się dokładnie określić ile liczba niewymierna wynosi!

Ale ja nie muszę wiedzieć, ile liczbowo wynosi liczba niewymierna.

Jeśli narysuję kwadrat o boku , to jego przekątna ma długość

I jest to na tyle dokładnie, na ile dokładnie da się narysować kwadrat o boku .

Mała ciekawostka obrazująca różnicę między konstrukcją teoretycznie poprawną, a konstrukcją dającą się realnie wykonać. W 1894 roku, niejaki Johann Gustav Hermes opisał (na 200 stronach) i zdeponował na uniwersytecie w Getyndze opis konstrukcji wielokąta foremnego o 65537 bokach. Konstrukcja zapewne jest poprawna ale nigdy nie zostanie wykonana.

bogdans napisał(a)

Konstrukcja zapewne jest poprawna ale nigdy nie zostanie wykonana.

Stworzenie robota rozumiejącego język ludzki oraz potrafiącego wykonywać konstrukcje geometryczne liczy się? Jeżeli tak, to nie byłbym pewien tego "nigdy" ;P

@Patryk27 miał więcej wyczucia.

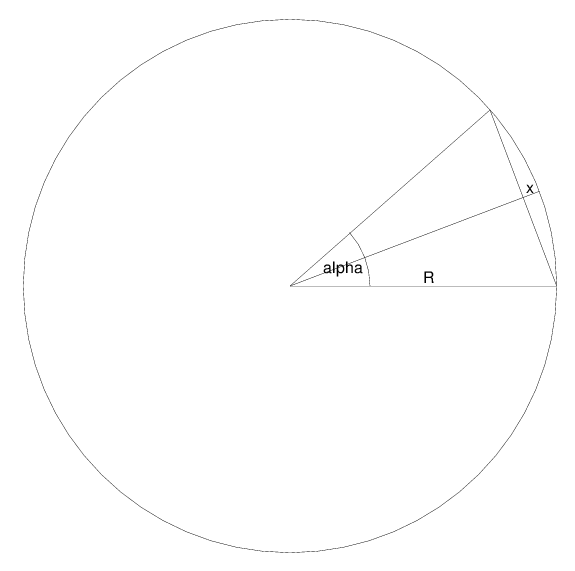
Istotna jest względna długość odcinka x. Dla 65537-kąta, , zatem .
Dla R=1000 metrów (bardzo duży plac), x to nieco więcej niż milimetr.