Chciałem dzisiaj pomyśleć nad tym zadaniem, ale niestety nie miałem zbyt dużo czasu, a jako że wygląda na to że @mariotti myśli równolegle ze mną to muszę się pośpieszyć i wrzucić na razie nieskończone efekty tego myślenia ;].
Chciałem się pochwalić jak znajdę jakiś dobry algorytm, ale na razie zdążyłem tylko naiwne praktycznie brute-force w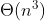 
:/. No ale konkurencja ściga, więc odpisuję teraz.
Algorytm naiwny - sprawdzanie wszystkich możliwych kombinacji i naiwne sprawdzanie czy zawierają punkty:
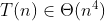
(etap: gotowe do implementacji)
To już sam zrobiłeś, nie ma się co nad tym rozwodzić ;).
Algorytm naiwny + jakaś drzewowa struktura danych - np. odpowiednie KD-drzewo jak @mariotti sugerował
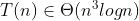
(etap: gotowe do implementacji)
Trochę kombinowania z napisaniem i testowaniem tego drzewa. W dodatku obawiam się że takie rozwiązanie wiele zysku nie przyniesie (fakt, złożoność lepsza, ale przy mniejszych n będzie odczuwalne mocne zwiększenie się niepozornej i zawsze pomijanej stałej - a większych n nie będzie, no bo przy złożoności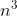 
i tak większe zbiory danych są nieosiągalne).
Algorytm dopasowywania punktu do odcinka
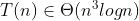
(etap: prawie gotowe do implementacji)
Rozważanie wszystkich możliwych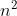 
odcinków i znalezienie do każdego z nich pasującego punktu. Chyba o to chodzi @mariotti -emu w ostatnim poście ;].
Rozważamy po kolei wszystkie 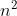par punktów (A, B). Sortujemy najpierw wszystkie punkty po odległości od prostej AB, i jeśli będziemy rozważać punkty od najbliższych do najdalszych to jesteśmy w stanie w czasie stałym sprawdzać czy kolejny punkt tworzy większy legalny trójkąt, oraz w czasie log(n) dodawać ten punkt do wykorzystywanej pomocniczej struktury danych.
Nad tym trochę myślałem, ale takie podejście nie ma przyszłości - poniżej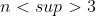 
log n sie nie da zejśc z powodu 
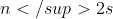ortowań n punktów.
Nie będę się nad tym więcej rozwodził bo mam lepszy algorytm, tylko się chwalę że coś tam jeszcze wymyśliłem ;].
Algorytm naiwny + naiwna struktuta danych - policzenie jakimś algorytmem dynamicznym ilości punktów wewnątrz dla każdego możliwego trójkąta
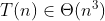
(etap: 'wydaje mi się')
Wydaje mi się że takie coś by było osiągalne w czasie stałym dla każdego trójkąta przez odpowiednie przetworzenie ich wstępnie i rozważanie w odpowiedniej kolejnosci 'wstępująco' - jak pisałem, 'wydaje mi sie', nie myślałem nad tym za dużo.
Algorytm naiwny + zamiatanie.
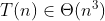
(etap: 'zaimplementowany')
Jak na razie najlepsze do czego doszedłem, a doszedłem do niego przed chwilą z herbatą i ołówkiem w ręce ;].
O co chodzi - jakaś skrócona lista kroków:
- sortujemy punkty po współrzędnej X (kwestia umowna oczywiście).
- przeglądamy po kolei punkty (będziemy rozważać trójkąty znajdujące się na prawo):
- bierzemy kolejny punkt, nazwijmy go A
- sortujemy kątowo wszystkie punkty z prawej strony (te z lewej możemy równie dobrze wywalać przy przechodzeniu na przykład) względem punktu A
- no i full naiwność (stąd niestety czas 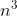) - bierzemy po kolei wszystkie punkty, w kolejności z sortowania kątowego, nazwijmy kolejny C
- bierzemy po kolei wszystkie punkty po B w kolejności z sortowania kątowego, nazwijmy kolejny taki punkt C
- możemy, znając
najgorszy możliwy odcinający kąt, sprawdzić w czasie stałym czy ABC zawiera jakiś trójkąt.
Daje to narodziny zaskakująco prostemu algorytmowi (mniej niż 50 linijek faktycznego kodu, żadnych skomplikowanych struktur danych)...
Jako że talk is cheap...
(ponad dwie godziny później. Jak zwykle zamotałem się przy znakach cross produktu oraz pół godziny walczyłem z prostym IO w pythonie. No ale wygląda na to że się udało)
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <vector>
#include <algorithm>
using namespace std;
struct point {
point() { }
point(int x, int y) :x(x), y(y) { }
int x, y;
};
struct cmp_by_x {
bool operator()(const point &a, const point &b) const {
return a.x < b.x;
}
};
int cross(const point &a, const point &b, const point &c) {
return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}
struct cmp_by_angle {
point base;
cmp_by_angle(point base) :base(base) { }
bool operator()(const point &a, const point &b) const {
return cross(base, a, b) > 0;
}
};
bool on_plane(point &a, point &b, point &c) { return cross(a, b, c) < 0; }
double area(point &a, point &b, point &c) { return abs(cross(a, b, c) / 2.0); }
point rnd_pt() { return point(rand() % 30, rand() % 30); }
int main() {
vector<point> pts(20); generate(pts.begin(), pts.end(), rnd_pt);
sort(pts.begin(), pts.end(), cmp_by_x());
double best = 0;
for (size_t i = 0; i < pts.size(); i++) {
vector<point> ang(pts.begin() + i + 1, pts.end());
sort(ang.begin(), ang.end(), cmp_by_angle(pts[i]));
for (size_t b = 0, cut = b; b < ang.size(); b++) {
for (size_t c = b + 1; c < ang.size(); c++) {
if (cut == b || !on_plane(ang[b], ang[cut], ang[c])) {
cut = c; best = max(best, area(pts[i], ang[b], ang[c]));
}
}
}
} printf("%.1f\n", best);
}
I... to tyle. Czas działania to okrągłe 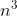(bo czasy sortowania sa dominowane przez przeglądanie wszystkich wierzchołków).
Napisałem też prosty (trywialny wręcz) skrypt w pythonie do wisualizowania punktów, żeby mieć pewność że pole (a ściśle, punkty na brzegach) są wyznaczane dobrze. Jeśli ktoś jest zainteresowany, wrzucę tutaj.
Zakładam że punkt wewnątrz trójkąta to nie punkt na jego krawędzi - jeśli tak nie jest, wystarczy zmienić < na <=.
No to tyle do tego algorytmu.
Algorytm mniej naiwny + zamiatanie.
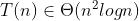
(etap: 'wydaje mi się')
Wydaje mi się, że sprawdzanie trójkątów wychodzących z punktu można zrobić lepiej niż w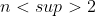 
. A ściśle, w n * log n (za pomocą jakiegoś podejścia dynamicznego), co dawałoby czas 
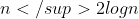- to już powoli zaczyna przypominać praktyczną złożoność (chociaż i tak bardzo sporą). Jak na razie mi się wydaje, spróbuję jutro nad tym pomyśleć w wolnym czasie.
Marzenia?
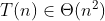
(etap: 'wydaje mi się')
Wydaje mi się, że ten problem da się rozwiązać jeszcze wydajniej, co najmniej 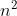(a może jeszcze lepiej?). To tylko intuicja, nawet jeśli się da być może nie wpadnę na to rozwiązanie ;].
