Algorytmy

Przeszukiwanie w głąb (DFS)

Thomashek

Przeszukiwanie w głąb, inaczej zwane DFS (ang. Depth-First Search), jest algorytmem służącym do przeglądania kolejnych wierzchołków grafu. Polega na przetwarzaniu krawędzi każdego, ostatnio odwiedzonego wierzchołka, który nie został wcześniej wywołany, dopóty, dopóki istnieją krawędzie prowadzące z tego wierzchołka. Po przeanalizowaniu wszystkich krawędzi prowadzących z danego wierzchołka, algorytm cofa się i przetwarza dalej, dotąd nie analizowane, krawędzie wierzchołka, z którego został wywołany. Operację należy wykonać na każdym, dotąd nie analizowanym wierzchołku (przy niektórych zastosowaniach jest to zbędne).

Przy niektórych zastosowaniach niezbędne jest zapamiętanie czasu odwiedzenia i czasu przetworzenia każdego wierzchołka (najczęściej każda operacja rozpoczęcia przetwarzania i końca przetworzenia zajmuje umownie jedną jednostkę czasu).

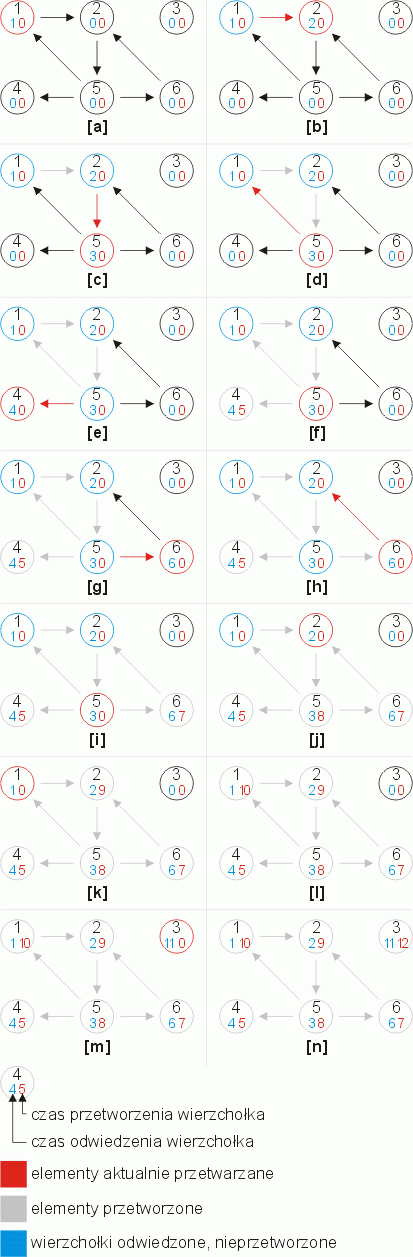
dfs.gif
Rys. 1. Działanie algorytmu przeszukiwania w głąb na przykładowym grafie

Czas działania algorytmu wynosi O(V+E), gdzie V to ilość wierzchołków oraz E to ilość krawędzi w analizowanym grafie.

Zastosowanie

Przeszukiwanie w głąb jest jednym z podstawowych algorytmów grafowych. Posiada szerokie zastosowanie. Jego zmodyfikowana wersja służy jako algorytm do znajdowania najkrótszej ścieżki pomiędzy źródłem a każdym wierzchołkiem (choć pesymistyczny czas działania nie jest zadawalający). Często jest używany do sprawdzenia, czy istnieje droga między wybranym wierzchołkiem (źródłem) a pozostałymi. Z przeszukiwania w głąb korzysta wiele innych algorytmów, w tym m. in.:

Implementacja

Poniżej podana przykładowa implementacja algorytmu (pseudokod), łącznie z przypisywaniem czasów odwiedzenia i przetworzenia każdego wierzchołka, co jest przydatne z kolei przy implementacji niektórych innych algorytmów wymienionych wyżej.

Główna procedura wygląda następująco:

<font name="Courier New">DFS ( wierzchołek )
{

czas = czas + 1
czas_odwiedzenia[wierzchołek] = czas
for każda krawędź wychodząca z wierzchołek do
{
if czas_odwiedzenia[wierzchołek, do którego prowadzi ta krawędź] == 0 then
{
wywołaj procedurę DFS( wierzchołek, do którego prowadzi ta krawędź )
}
}
czas = czas + 1
czas_przetworzenia[wierzchołek] = czas

}</span>

Warunek wewnątrz pętli dokonuje sprawdzenia, czy wierzchołek, do którego prowadzi krawędź, nie został już odwiedzony, gdyż zgodnie z opisem algorytmu, procedurę należy wywołać tylko jeden raz dla każdego wierzchołka. Powyższą procedurę należy wywołać dla każdego wierzchołka grafu, którego czas_odwiedzenia jest równy 0 (w przypadku, gdy graf nie jest spójny).

Jeśli nie jest wymagane zapamiętanie czasu odwiedzenia i przetworzenia każdego wierzchołka, należy pominąć przy implementacji dwie pierwsze i dwie ostatnie linie pseudokodu wewnątrz procedury DFS.

Przy sprawdzaniu, czy istnieje droga z danego wierzchołka do pozostałych, należy wywołać procedurę DFS tylko dla wierzchołka źródłowego, a wewnątrz pętli zamieścić warunek przerywający operację przeszukania, gdy zostanie odwiedzony wierzchołek docelowy. Jeśli nie nastąpi przerwanie przeszukiwania, oznacza to, iż droga pomiędzy tymi wierzchołkami nie istnieje.

Algorytmy

4 komentarzy

Później dodam jeszcze ładny obrazek do tego artykułu.

EDIT: Dodałem.

PS. Niech ktoś skasuje Image:dfs.jpg (za duży był, zmieniłem na gifa).

Spoko, fajne, przydalby sie jedynie przyklad jakis praktyczny (albo w C albo w Pascalu).

Ma ktoś to napisane w Pascalu??

/
Program który wyświetla koszt Minimalnego Drzewa Rozpinającego
dane wczytywane z pliku tekstowego
/
#include<algorithm>
#include <fstream>
#include <conio.h>
#include <iostream>
#include <string.h>
#include <vector>
using namespace std;
int tab[7000], ile[7000]; // 7000 - to liczba wszystkich elementów
int fa;
int Find(int a) { return (tab[a]==a) ? a : (tab[a] = fa); }
const int MAX = 10;
char wiersz[MAX];
FILE*plik=fopen("c:\lista.txt","r");
bool Union(int a, int b)
{
int fa = Find(a); // szukaj reprezentanta zbioru zawierającego element 'a'
int fb = Find(b); // szukaj reprezentanta zbioru zawierającego element 'b'

if (fa==fb) return false; // nie trzeba nic łączyć
if (ile[fa] <= ile[fb])
{
    ile[fb] += ile[fa];
    tab[fa] = fb;
}
else
{
    ile[fa] += ile[fb];
    tab[fb] = fa;
}
return true;

}

pair< int,pair<int,int> > Edges[300000]; // tablica krawędzi do posortowania

int main(void)
{

int n, m, a,b,c,cost=0;
scanf("%d %d", &n, &m);// n to liczba wierzchołków, m liczba krawędzi
for (int i=0; i<n; i++)
{
    tab[i] = i; 
    ile[i] = 1; 
}

//ifstream plik_odczyt("c:/lista.txt");
fopen("c:\lista.txt","r");
for (int i=0; i<m; i++)
{
plik_odczyt << ("%d %d %d", &a, &b, &c); a--; b--;; wierzchołki i ich waga
fscanf(plik, "%d %d %d", &a, &b, &c);a--; b--;
Edges[i] = make_pair( c, make_pair(a,b) );
}
sort(Edges, Edges+m);
for (int i=0; i<m; i++)
if ( Union(Edges[i].second.first,Edges[i].second.second) )
{
cost += Edges[i].first;
// krawędz drzewa : Edges[i].second.first -- Edges[i].second.second
}
fclose(plik); 

printf("%d\n", cost);
system("pause");

}

Bardziej obcykani poprawią sobie te błędy