---

Konwersja do składni Coyote robiona ręcznie, więc pewne błędy (np. złe formatowanie, brak ilustracji etc) mogłem przeoczyć.
Jeśli to możliwe, polecam z tekstem zapoznawać się z oryginalnego dokumentu: ray.2.pdf

---

Raytracing: krok po kroku

cz. 2 - realistyczna kamera

I. Co/Dlaczego?

W tej części zaimplementowana zostanie kamera perspektywiczna dająca znacznie bardziej realistycznie wyglądające wyniki oraz bliższa temu jak my, ludzie, widzimy świat.

II. Różnice

W kontekście grafiki komputerowej, projekcja to transformacja trójwymiarowych punktów na płaską powierzchnię - zwaną w kontekście raytracingu view plane. Punkty są transformowane wzdłuż prostych zwanych projektorami.

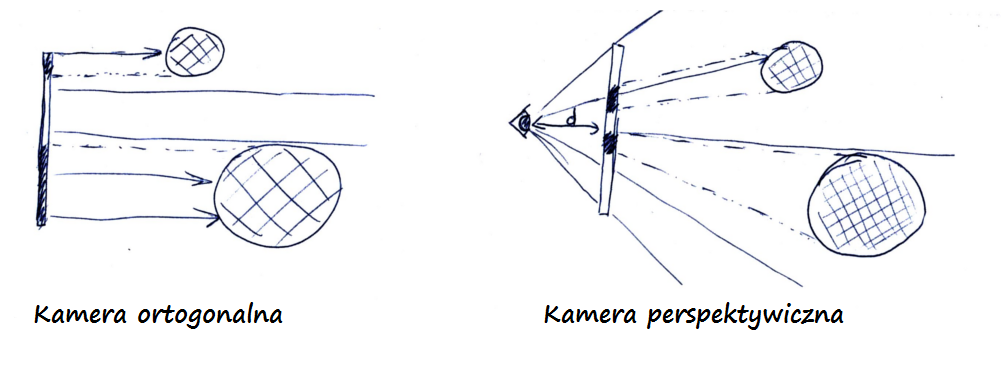
W projekcji ortogonalnej wszystkie projektory są równoległe (mają taki sam kierunek), ale zaczynają się w różnych punktach.
Dla kontrastu, w projekcji perspektywicznej każdy projektor ma inny kierunek, ale wszystkie zaczynają się w jednym punkcie (zwanym center of projection, centrum projekcji).
Wpływa to w istotny sposób na renderowanie.Właściwości kamery perspektywicznej to:
Obiekty wydają się zmniejszać wraz ze zwiększaniem się odległości do oka.
Równoległe linie będące jednocześnie nierównoległe do view plane zbiegają się w jednym punkcie na obrazie.
Równoległe linie będące jednocześnie równoległe do view plane pozostają równoległe.

III. Implementacja

Do reprezentowania dowolnej kamery używamy bardzo ogólnego interfejsu ICamera (to pierwszy moment kiedy okazał się on przydatny). Dla mających słabą pamięć, przypomnienie:

interface ICamera
{
    Ray GetRayTo(Vector2 relativeLocation);
}

Żeby dodać nową kamerę wystarczy stworzyć klasę implementującą ten interfejs.

Transformację perspektywiczną możemy opisać za pomocą następujących parametrów:
Dowolna pozycja oka (z tego punktu wychodzą wszystkie promienie).
Dowolny kierunek patrzenia
Dowolna orientacje względem kierunku patrzenia (reprezentowany za pomocą wektora up wzkazującego w górę).
Dowolna odległość od pozycji oka do view plane.

Możemy w tym momencie stworzyć szkielet klasy kamery perspektywicznej, pobierający parametry których będzie potrzebować:

class PinholeCamera : ICamera
{
    Vector3 origin;
    Vector3 lookAt;
    Vector3 up;
    double distance;

    public PinholeCamera(Vector3 origin, Vector3 lookAt, 
        Vector3 up, double distance)
    {
        this.origin = origin;
        this.lookAt = lookAt;
        this.up = up;
        this.distance = distance;
    }

    public Ray GetRayTo(Vector2 relativeLocation)
    {
        return new Ray(origin, RayDirection(relativeLocation));
    }

    Vector3 RayDirection(Vector2 relativeLocation)
    {
        // wyznaczanie kierunku promienia
        throw new System.NotImplementedException();
    }
}

IV. Bazy Ortonormalne
Teraz niestety trochę matematycznej magii. Wszystkie parametry kamery są koordynatami w przestrzeni świata, ale kamera potrzebuje swojego własnego systemu współrzędnych. Jest on określony za pomocą tak zwanej bazy ortonormalnej.
Trzy wektory (u, v, w) tworzą bazę ortonormalną jeśli mają następujące własności:
Wszystkie wektory są znormalizowane (długość == 1)
Są wzajemnie prostopadłe
Tworzą razem prawoskrętny układ współrzędnych ( w = u × v)

Na przykład wektory u= [1, 0, 0] v= [0, 1, 0] i w=[0, 0, 1] to baza ortonormalna przestrzeni euklidesowej.

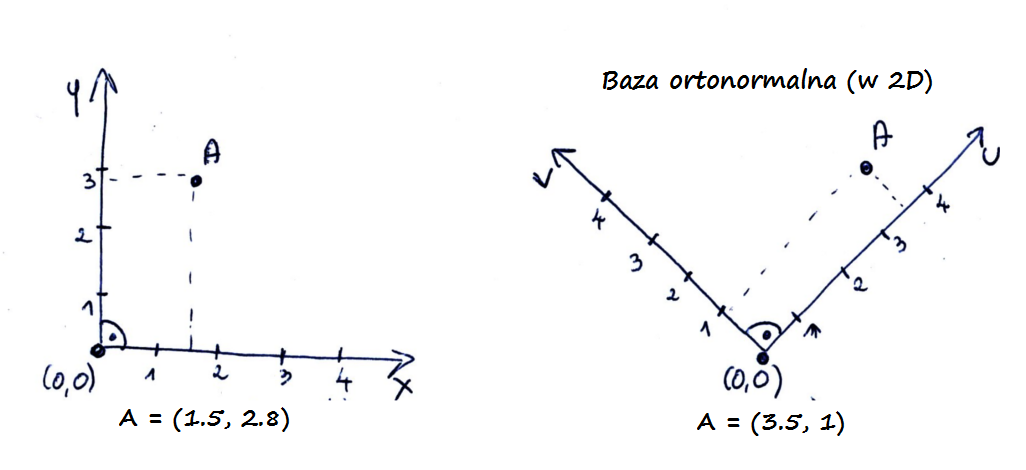
Baz ortonormalnych używamy w raytracingu wszędzie tam gdzie potrzebujemy lokalnego systemu współrzędnych (na przykład przy kamerach, ambient occlusion, glossy reflection itd).

Bazę można skonstruować z dwóch dowolnych wektorów a i b (nie muszą być wzajemnie prostopadłe ani znormalizowane).

Pierwszym krokiem jest stworzenie wektora w - jest to zmormalizywany wektor równoległy do a.
Następnie obliczany jest wekor u będący znormalizywanym iloczynem wektorowym b×w.
Ostatecznie v jest równy (w×u) tworząc w ten sposób prawoskrętny system współrzędnych.

w = a / |a|
u = (b×w) / |b×w|
v = w×v

Ok, wiemy już jak tworzyć ONB, teraz pozostaje zasadnicze pytanie, do czego nam to właściwie potrzebne? Otóż mając do dyspozycji ONB kamery (u, v, w), pozycję punktu na viewplane (x, y), oraz odległość viewplane od oka (d) możemy łatwo wyliczyć kierunek promienia wychodzącego z kamery jako
dir = xu+yv+dw

Teraz możemy zapisać to w kodzie:

class OrthonormalBasis
{
    Vector3 u;
    Vector3 v;
    Vector3 w;

    public OrthonormalBasis(Vector3 eye, Vector3 lookAt, Vector3 up)
    {
        w = eye - lookAt;
        w = w.Normalized;
        u = Vector3.Cross(up, w);
        u = u.Normalized;
        v = Vector3.Cross(w, u);
    }

    public static Vector3 operator *(OrthonormalBasis onb, Vector3 v)
    {
        return (onb.u * v.X + onb.v * v.Y + onb.w * v.Z);
    }
}

V. Implementacja 2
Mając do dyspozycji narzędzie jakim są bazy ortonormalne, stworzenie kamery perspektywicznej jest trywialne:

class PinholeCamera : ICamera
{
    OrthonormalBasis onb;
    Vector3 origin;
    double distance;

    public PinholeCamera(Vector3 origin, Vector3 lookAt,
        Vector3 up, double distance)
    {
        this.onb = new OrthonormalBasis(origin, lookAt, up);
        this.origin = origin;
        this.distance = distance;
    }

    public Ray GetRayTo(Vector2 relativeLocation)
    {
        return new Ray(origin, RayDirection(relativeLocation));
    }

    Vector3 RayDirection(Vector2 v)
    {
        return onb * new Vector3(v.X, v.Y, -distance);
    }
}

Gotowe, teraz możemy użyć kamery i cieszyć się nowymi widokami:

ICamera camera = new PinholeCamera(new Vector3(0, 1, -8),
    new Vector3(0, 0, 0),
    new Vector3(0, -1, 0),
    1);

Dla lepszego efektu warto również przestawić obiekty na scenie:

// Trzy różnokolorowe kule
world.Add(new Sphere(new Vector3(-4, 0, 0), 2, Color.Red));
world.Add(new Sphere(new Vector3(4, 0, 0), 2, Color.Green));
world.Add(new Sphere(new Vector3(0, 0, 3), 2, Color.Blue));

Oto efekt naszych starań:

Przy pewnej ilości wyobraźni można sobie wyobrazić że te kolorowe kółka na obrazku reprezentują kontury trójwymiarowych kul rzutowanych na płaszczyznę. Przede wszystkim warto zauważyć że najdalsza (niebieskia) kula wydaje się najmniejsza - perspektywa, panie! Ich prawdziwe piękno wydobędziemy dopiero za pomocą światła i cienia, ale wcześniej zajmiemy się czymś znacznie prostszym...