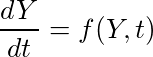O ile podstawy czy nawet odczyt plików w miarę ogarnąłem, tak niestety wykresy na razie sprawiają mi trudność.
Zadanie wygląda tak:
**Wyznacz ruch dwóch ciał połączonych sprężynami o sztywności k=10 znajdujących się polu grawitacyjnym o przyśpieszeniu g⃗ =[0,−9.81][ms2]. Oba ciała są wstępnie ustawione w odległości l=10 od siebie i leżą na linii poziomej, a sprężyna w tym momencie jest nienaciągnięta. Prędkość początkowa ciała pierwszego wynosi u1=[0,5][ms] a drugiego $ u_2=[-3,3] []$. Masy obu ciał są równe i wynoszą m=1[kg] lub m=10[kg] (sprawdź jak zmienią się wyniki w obu przypadkach). Wykonaj wykres torów ruchu obu ciał, a następnie utwórz animację, w której przedstawisz ruch ciał w postaci punktów poruszających się po obliczonych torach. **
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation
k=10
l=10
m_1=1
m_10=10
kroki=500
czas_poczatek=0
czas_koniec=10
lokalizacja_a = [0,0]
lokalizacja_b = [-l,0]
predkosc_a=[0,0.5]
predkosc_b=[-3,3]
grawitacja=9.81
tablica=np.linspace(czas_poczatek,czas_koniec,kroki+1)
dt=tablica[1]-tablica[0]
przyspieszenie=np.zeros((kroki+1,2))
I co dalej?
Dane mam, ale jakim wzorem je ogarnąć? Jakąś funkcję trzeba stworzyć?
Może chodzi o coś takiego: https://pl.wikipedia.org/wiki/Algorytm_Verleta