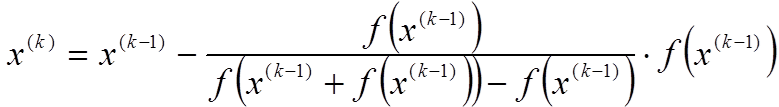Witam,
Mam problem z działaniem prostego programu obliczającego pierwiastek funkcji nieliniowej z wykorzystaniem metody iteracji prostej.
Funkcja jest następująca:
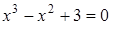
a kod programu wygląda tak:
#include "stdafx.h"
#include "stdio.h"
#include "conio.h"
#include "math.h"
double x1; // x1 - punkt poczatkowy, od ktorego rozpoczynamy obliczenia
double x2; // x2 - poszukiwany pierwiastek
double blad=0.001; // blad - blad przyblizenia
double wynik; // wynik - zmienna pomocnicza, jej wynik jest brany do warunku petli
double funkcja(double x) // wartosc przeksztalconej funkcji
{
return pow(x,2)+3/x ; // Przeksztalcona funkcja poczatkowa
}
int main()
{
x1=1; // punkt poczatkowy
do
{
x2=funkcja(x1); // wartosc pierwiastka
wynik=fabs(x2-x1); // blad, petla jest wykonywana dopoki jest on wiekszy od bledu przyblizenia
x1=x2; // nowa wartosc punktu startowego
}
while(wynik>=blad);
printf("Poszukiwany pierwiastek to x= %lf",x2);
getch();
return 0;
}
Wynik:

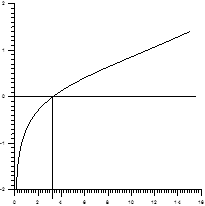
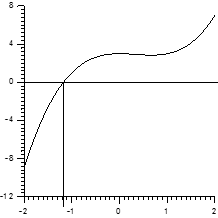
Jak widać na wykresie jest pierwiastek w punkcie około -1, a wynik jest zupełnie inny.
Czy wie ktoś w czym leży problem?
Proszę o pomoc :)
Pozdrawiam