Witajcie,
Potrzebuję zrobić mniej więcej coś takiego:
jednak nie może to być zwykła bitmapa ponieważ w zależności od rozmiaru okna i skali, którą użytkownik wybierze może się to zmienić np tak:
Na ten moment jedyne wyjście jakie widzę to rysowanie po canvasie tym bardziej, że później podając kąt i odległość będę miał na tym wykresie coś zaznaczyć. Macie pomysł jak to uzyskać inaczej niż poprzez zwykłe dzierganie po canvasie?
Jeśli ma się skalować to zdecydowanie rysowanie samodzielnie da najlepsze efekty.
Możesz jeszcze przygotować grafikę SVG w jakimś programie graficznym ale czy potem "wstrzelisz" się w skalę to już kolejny problem.
Pytanie jest inne - co jest złego w rysowaniu po canvasie? Czemu chcesz to zmienić, jeśli to działa i jest OK? Czy chodzi Ci raczej o samą zamianę - żeby np. rysować nie bezpośrednio na canvas ale na jakiejś bitmapie w pamięci, a potem przerzucanie tego na formatkę?
Wydaje mi się, że jeśli chcesz to skalować, to najlepszą opcją jest właśnie wydzielenie tego do osobnej procedury, a potem jej wywołanie. Ona jako parametry pobierze rozmiar okna/elementu na którym ma rysować, a potem wymaluje siatkę dopasowaną do danej sytuacji.
Ewentualnie, jak pisał @katakrowa - zrobić grafikę w formie wektorowej. ale nie wiem, czy taka zabawa ma sens. Bo potem jakbyś chciał cokolwiek zmienić, to nie w kodzie, tylko pojawi się konieczność edycji tego pliku graficznego - więc moim zdaniem, lepiej to rysować na bieżąco w kodzie.
Po prostu jest to dużo roboty (grafiki załączone w temacie są w najprostszej postaci) i zastanawiam się czy jest jakieś np gotowe narzędzie do takich zabaw.
cerrato napisał(a):
Ewentualnie, jak pisał @katakrowa - zrobić grafikę w formie wektorowej. ale nie wiem, czy taka zabawa ma sens. Bo potem jakbyś chciał cokolwiek zmienić, to nie w kodzie, tylko pojawi się konieczność edycji tego pliku graficznego - więc moim zdaniem, lepiej to rysować na bieżąco w kodzie.
W sumie z SVG **też trzeba liczyć skalę **żeby nałożyć dane na siatkę. A skoro już mamy tą skalę policzoną to narysowanie kilku kresek jest chyba najmniejszym problemem.
Pomijając to, że prawdopodobnie i tak przydało by się jakieś kątowe odwzorowanie danych po praca z danymi kątowymi na osiach x/y może być upierdliwa...
Tak czy siak ja bym zrobił następująco.
class classAngleChart{
setWidth( x ){}
setHeight( y ){}
setCenter( x,y ){}
setMaxRadius( x,y ){}
setVisibleAngle( x,y ){ określa wycinek okręgu do wyświetlenia }
getXYl( angle, radiusr ){ klasa przelicza kąt i promień na pozycję piksela w układzie X/Y }
}
I dopiero mając takie cuś brałbym się za dalsze rysowanie.
Oczywiście gotowce są także dostępne:
https://www.google.com/search?q=radar++chart+Javascript
Pytanie czy szybciej napiszesz to sam czy szybciej nauczysz się używać gotowca...
Na potrzeby samodzielnego rysowania wszystko masz tutaj:
woolfik napisał(a):
Po prostu jest to dużo roboty […]
Eee tam dużo. Kształt bazowy malujesz metodami Pie (tło i obramowanie całości), a resztę wewnątrz malujesz w pętli metodami Arc i Line (albo Pie i Line, choć wolałbym w kółko tła nie wypełniać, bo to bez sensu). Obliczenia współrzędnych są bardzo proste — możesz skorzystać z tych dotyczących ruchu po okręgu, bo znany jest punkt początkowy, kąt oraz odległość:
DestX := SourceX + Cos(Angle) * Radius;
DestY := SourceY + Sin(Angle) * Radius;
Całość fajnie ilustruje poniższa animacja:
Źródło: https://commons.wikimedia.org/wiki/File:Circle_cos_sin.gif
Jeśli potrzebujesz ”ścisnąć” radar, to wystarczy zadany kąt wstępnie pomnożyć przez jakiś współczynnik (mniejszy od 1 zmniejszy kąt wyjściowy, a większy od 1 go powiększy). Dosyć prosta sprawa, ale pamiętaj, że te obliczenia robi się na radianach. W razie czego kąty konwertuj sobie za pomocą funkcji DegToRad i RadToDeg.
Ja bym się szarpnął na własnoręczne renderowanie tego radaru. ;)
Dobra Panowie mam jeszcze jeden mały problem, z którym może mi coś podpowiecie bo nie do końca kumam z czego wynika problem (tzn. domyślam się, że chodzi o współrzędne punktów dla krzywej beziera) ale nie do końca wiem jak je przeliczyć aby się zgadzało. Mianowicie poniższy kodzi:
type
TPoints = array of TPoint;
procedure TForm1.Button2Click(Sender: TObject);
var
cp: TPoint;
x, y: integer;
scala: integer;
aP: TPoints;
i: Integer;
begin
SetLength(ap,13);
scala := SpinEdit1.Value;
PaintBox1.Canvas.FillRect(PaintBox1.ClientRect);
cp := Point(round(PaintBox1.Width/2),round(PaintBox1.Height/2));
for i := 0 to 12 do
begin
ap[i].x := cp.X + Round(scala * cos(DegToRad(spnKat.Value-150 + i * 10))); //minus 150 aby się dla 0 rysowało względem nazwijmy to północy :)
ap[i].Y := cp.y + Round(scala * sin(DegToRad(spnKat.Value-150 + i * 10)));
PaintBox1.Canvas.Pen.Color := RGB(Random(255),Random(255),Random(255));
PaintBox1.Canvas.MoveTo(cp.X,cp.y);
PaintBox1.Canvas.LineTo(ap[i].X,ap[i].Y);
end;
PaintBox1.Canvas.PolyBezier(ap);
end;
daje taki efekt:
Jak widać częśc punktów pokrywa się z osią ale niektóre nie. Możecie coś podpowiedzieć? Załączam demo i wołam @furious programming :)
woolfik napisał(a):
Dobra Panowie mam jeszcze jeden mały problem, z którym może mi coś podpowiecie bo nie do końca kumam z czego wynika problem (tzn. domyślam się, że chodzi o współrzędne punktów dla krzywej beziera) […]
Coś ta krzywa jest mało Bezierowa — wygląda bardziej jak PolyLine niż PolyBezier… A pisałem, że Pie jest lepszy. :D
Utrudniasz sobie trochę robotę. Owszem, można obramowanie całości namalować za pomocą krzywej i dwóch prostych, ale to kupka zbędnych obliczeń, no i tło trzeba wypełnić później metodą FloodFill. A tak to wystarczy ustawić kolory ramki oraz tła i wywołać jedną metodę Pie, która od razu stworzy główny kształt wycinka.
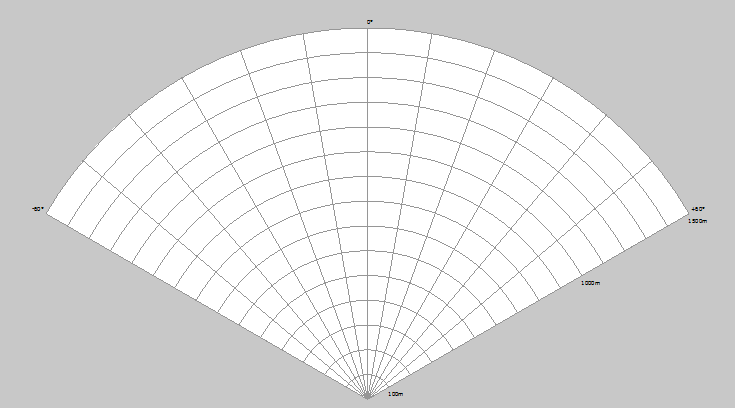
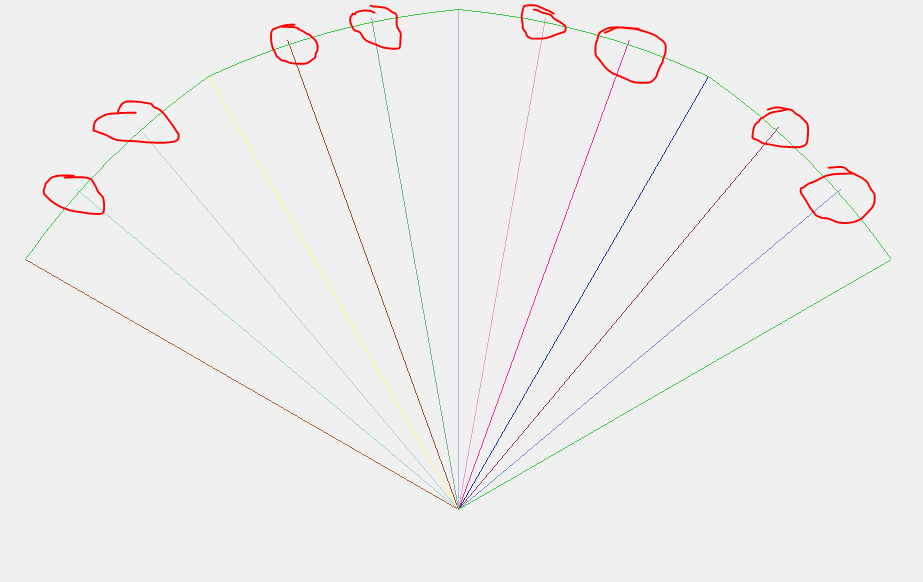
Jak widać część punktów pokrywa się z osią ale niektóre nie.
Nie mam pojęcia dlaczego tak się dzieje, ale problemem nie jest długość promieni, a kształt krzywej — ta nie układa się w okrąg, miejscami jest spłaszczona. Dlatego na Twoim miejscu olałbym te krzywe i skorzystał z Pie, bo jest znacznie prostszy w użyciu i faktycznie tworzy wycinek koła, bez żadnych spłaszczeń i innych mankamentów.
No dobra, teraz rozwiązanie — w załączniku masz źródła oraz skompilowanego exeka do zabawy. Apka pisana w Lazarusie, bo Delphi nie używam i nie mam go zainstalowanego, ale kod możesz przenieść do Delphi bez żadnych zmian.
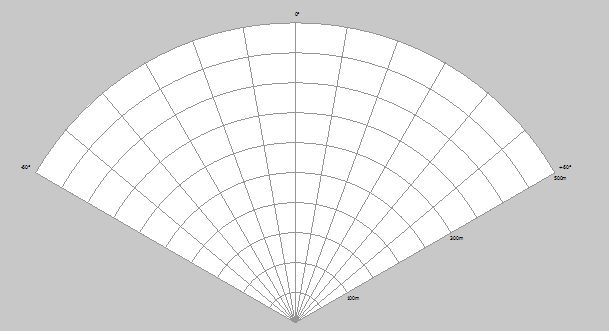
Jak sugerowałem, najłatwiejszym sposobem na namalowanie wycinka koła jest użycie Pie, z odpowiednio obliczonymi kątami. Można to zrobić na dwa sposoby — albo w pętli wołać Pie i oprócz głównego kształtu, namalować od razu jego pierścienie, albo metodą Pie namalować główny kształt, a metodami Arc domalować pierścienie. Pierwsza opcja łatwiejsza, ale powoduje, że linie graniczne kształtu miejscami będą pogrubione. Druga pozwala uniknąć tego defektu, ale wymusza napisanie większej ilości kodu.
Na potrzeby testu, skorzystałem z tej pierwszej, czyli kształt i pierścienie renderowane są za pomocą Pie w pętli:
procedure TMainForm.DrawRadarRings();
var
PieIndex, PiesCount, PieRadius: Integer;
PieStep: Single;
begin
PiesCount := FRadarRangeDistance div 100;
PieStep := FRadarRadius / PiesCount;
for PieIndex := PiesCount downto 1 do
begin
PieRadius := Round(PieIndex * PieStep);
MainForm.Canvas.Pie(
FRadarSpot.X - PieRadius,
FRadarSpot.Y - PieRadius,
FRadarSpot.X + PieRadius,
FRadarSpot.Y + PieRadius,
FRadarSpot.X + Round(PieRadius * Cos(DegToRad(90 - FRadarRangeAngle))),
FRadarSpot.Y - Round(PieRadius * Sin(DegToRad(90 - FRadarRangeAngle))),
FRadarSpot.X + Round(PieRadius * Cos(DegToRad(90 + FRadarRangeAngle))),
FRadarSpot.Y - Round(PieRadius * Sin(DegToRad(90 + FRadarRangeAngle)))
);
end;
end;
Pole FRadarRangeAngle zawiera kąt będący wielokrotnością 10, z zakresu od 10 (minimalny wycinek koła) do 180 (pełne koło). Użycie kąta 90 pozwala ustawić kąt 0° na północ, a nie jak domyślnie na wschód. Wycinki renderowane są od największego do najmniejszego, tyle razy ile radar ma mieć pierścieni dystansowych. Maksymalny dystans trzymany jest w polu FRadarRangeDistance, zakres od 100 do 3000 (w mojej testowej aplikacji, można ustawić dowolny niezerowy).
Tak więc najpierw oblicza się liczbę pierścieni, dzieląc dystans przez 100. Następnie oblicza się grubość pierścienia, dzieląc promień radaru ze zmiennej FRadarRadius przez liczbę pierścieni. Wynik trzymany jest w postaci zmiennoprzecinkowej, aby uniknąć błędu zaokrąglenia. Następnie w pętli od największego do najmniejszego pierścienia, najpierw oblicza się promień wycinka mnożąc indeks pierścienia przez jego grubość (całość zaokrągla się na koniec), a następnie renderuje wycinek o zadanych kolorach tła i obramowania. Mniejsze wycinki przykrywają większe, co daje docelowo cały wycinek oraz linie pierścieni.
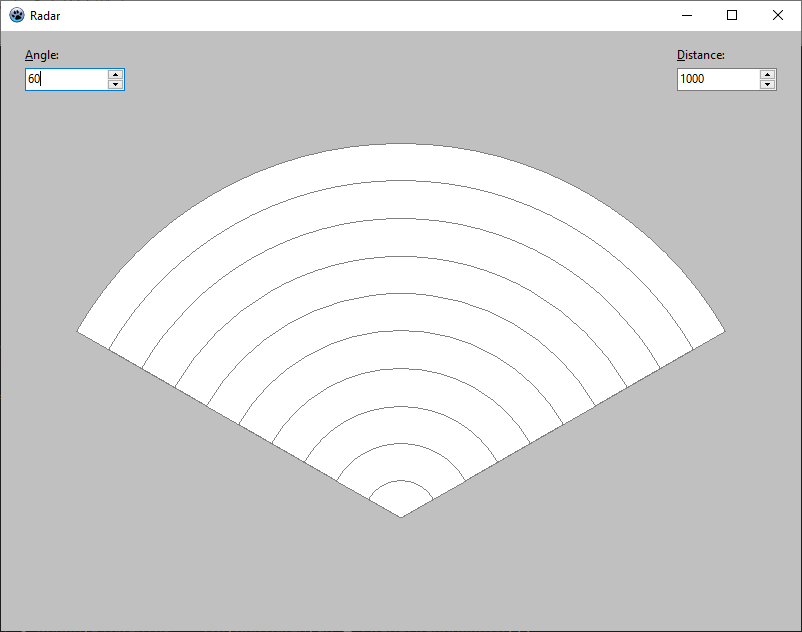
Druga część to renderowanie linii sekcji według kątów:
procedure TMainForm.DrawRadarSections();
var
LineIndex, LinesCount: Integer;
begin
LinesCount := (FRadarRangeAngle div 10) * 2 - 1;
for LineIndex := 1 to LinesCount do
MainForm.Canvas.Line(
FRadarSpot.X,
FRadarSpot.Y,
Round(FRadarSpot.X + Cos(DegToRad(270 + FRadarRangeAngle - LineIndex * 10)) * FRadarRadius),
Round(FRadarSpot.Y + Sin(DegToRad(270 + FRadarRangeAngle - LineIndex * 10)) * FRadarRadius)
);
end;
Najpierw oblicza się liczbę linii do namalowania. Zakres kątowy dzieli się przez 10, uzyskując liczbę wycinków, mnoży się ją przez 2 aby dostać liczbę pól po obu stronach kąta 0° i odejmuje 1, aby nie renderować linii na brzegu głównego wycinka (coby uniknąć sztucznego pogrubienia). To by miało znaczenie przy używaniu Arc, ale że używam Pie, to nie ma to znaczenia. Jednak jeśli wymieni się Pie na Arc, to powyższy kod się dostosuje.
No i tyle — w pętli renderuje się linie w kierunku odwrotnym do wskazówek zegara, zaczynając od kąta o 10° mniejszego niż kąt brzegowy.
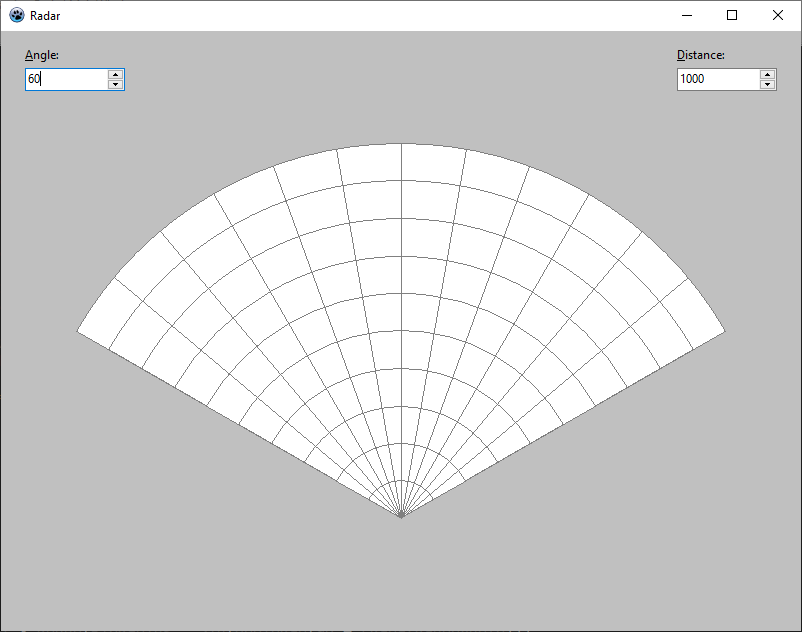
Aplikację testową przygotowałem w taki sposób, że renderowanie radaru jest sparametryzowane — w dwóch kontrolkach edycyjnych ustala się zakres kątowy (rozmiar wycinka) oraz zakres dystansowy (liczba pierścieni), dzięki czemu można sprawdzić jak wygląda wykres dla różnych danych wejściowych.
Co prawda parametryzacja jest uboga, bo zakres kątowy jest wielokrotnością 10, a dystansowy 100, ale na potrzeby testu wystarczy. W razie czego łatwo ten kod przystosować do dowolnych zakresów kątowych i dystansowych, zamieniając w kodzie niektóre literały na wartości ustalane dynamicznie.
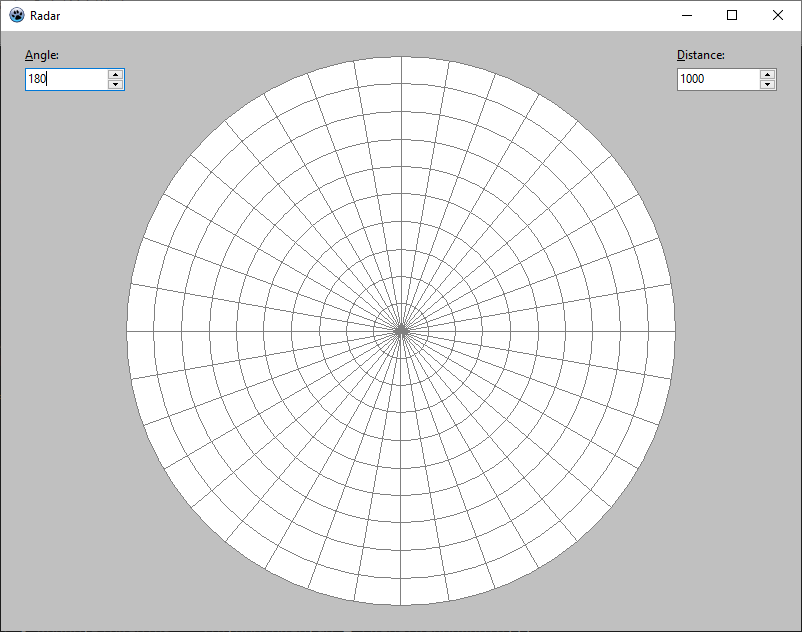
Nie wykryłem żadnych problemów z obliczaniem i renderowaniem promieni — te nie są ani za krótkie, ani za długie. Tak więc spokojnie możesz z tego kodu skorzystać i przystosować go do własnego projektu. Ale i tak sugeruję wymienić pętle z Pie na jedno wywołanie Pie i pętlę Arc — wykluczy się sztuczne pogrubienie promieni brzegowych.
No, to 200zł się należy. :P
Straszna pikseloza na tym wykresie, może lepiej skorzystać z biblioteki GDI+, która potrafi malować z antyaliazingiem, no i tam są metody do malowania krzywych Beziera.
@marogo: to co widać na moich zrzutach jest renderowane za pomocą GDI+, bo to z natury antialiasingu nie obsługuje — ani dla kształtów, ani dla skalowania obrazów. Oczywiście to tylko aplikacja testowa, w której liczy się algorytm renderowania, nie jakość detali.
W docelowym projekcie można użyć biblioteki firm trzecich i to co podlinkowałeś jest dobrym rozwiązaniem. Natomiast w Lazarusie skorzystałbym z pakietu BGRABitmap, bo ma mnóstwo ficzerów, z filtrami włącznie. :P
Svg
@renderme: radar docelowo ma być dynamicznie renderowany, na podstawie kąta i odległości, dlatego SVG odpada.
marogo napisał(a):
Straszna pikseloza na tym wykresie, może lepiej skorzystać z biblioteki GDI+, która potrafi malować z antyaliazingiem, no i tam są metody do malowania krzywych Beziera.
Tak, ale GDI+ jest wolne (a co do jego akceleracji czy nie, to już sam MS mam wrażenie się pogubił i to ostro) - tylko do tego co tam widzę, to wystarczy aż nadto.
Ale gdyby tego rysowania było więcej, albo istnieje potencjał na dodawanie nowych i nowych efektów a może bardziej złożonych wykresów, to być może najlepiej użyć Graphics32.
Jest o rząd wielkości (co najmniej) szybszy i oferuje nieporównywalnie większe możliwości niż GDI/GDI+.
A takie "bzdurki" jak wygładzanie krawędzi czy przezroczystość (a nawet implementacja warstw) są tam dostępne by design.
Jak jechać na full to OpenGl i cześć - będziesz mógł obracać w 3D te... kreski i łuczki. :)