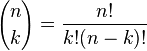mwili ładnie policzył, że:

Jeśli m>n/2 to możemy przyjąć m=n-m a wynik się nie zmieni.
Przyszedł mi pomysł do głowy jak można to maksymalnie poskracać. Należy każdy czynnik po kolei rozłożyć na czynniki pierwsze. Czynniki zapisywać w tablicy, gdzie indeks komórki to kolejny indeks czynnika w tablicy liczby pierwszych. Każdy czynnik z licznika zwiększy wartość komórki o 1, z mianownika zmniejszy. Na samym końcu w tablic powinny nam pozostać jedynie liczby dodatnie - ilość mnożeń jaką musimy wykonać danym czynnikiem pierwszym. Zademonstruje na przykładzie:
pierwsze[] = { 2, 3, 5, 7, ... } - tablice tą powiększamy w miarę potrzeb podczas działania programu.
czynniki[] = { 0 , 0, 0, 0, ... } - tablica na czynniki pierwsze, powiększamy o zerowe komórki w miarę potrzeb, indeks komórki w tej tablicy odpowiada indeksowi czynnika w tablicy liczb pierwszych.
Aby uniknąć realokacji pamięci, rozmiary tablicy możemy oszacować, musimy przybliżyć ilość liczb pierwszych z zakresu od 1 do n (istnieją do tego funkcje matematyczne, np. punkcja PI) i dodać jakiś zapas.
n = 10, m = 6
(n po m) = 78910 / 1234
licznik = 78910
mianownik = 23*4
mianownik - odejmujemy
Rozkładamy 2 na czynniki pierwsze, dostajemy 2, czynniki = { -1, 0, 0, 0 }
Rozkładamy 3 na czynniki pierwsze, dostajemy 3, czynniki = { -1, -1, 0, 0 }
Rozkładamy 4 na czynniki pierwsze, dostajemy 2^2, czynniki = { -3, -1, 0, 0 }
teraz licznik - dodajemy
Rozkładamy 7 na czynniki pierwsze, dostajemy 7, czynniki = { -3, -1, 0, 1 }
Rozkładamy 8 na czynniki pierwsze, dostajemy 2^3, czynniki = { 0, -1, 0, 1 }
Rozkładamy 9 na czynniki pierwsze, dostajemy 3^2, czynniki = { 0, 1, 0, 1 }
Rozkładamy 10 na czynniki pierwsze, dostajemy 2*5, czynniki = { 1, 1, 1, 1 }
Wynik to 21315171 = 2357.
Dodatkowo warto pamiętać niektóre rozkłady (na tyle na ile nam pamięć pozwoli). Przyspieszy to obliczenia. Bo jeśli rozkładając jakaś liczbę rozłożymy ją na liczbę już wcześniej rozłożoną to możemy skorzystać z już wcześniej wyznaczonego rozkładu.
Np. rozkładamy 30=215=235, zapamiętujemy. Gdzieś później rozkładamy 120, dostajemy 120=260=2230 i tu skorzystamy z zapamiętanej 30-stki 120=2230=22235
Rozkład na czynniki pierwsze:
#include <iostream> //cin, cout
#include <cmath> //sqrt
#include <cstdlib> //system
using namespace std;
//uwaga, 3-ka jest jeszcze nie wyznaczona, jej obecność w tablicy jest wymaga do
//prawidłowego dziłania funkcji nastepnaPierwsza podczas jej pierwszego wywołania
unsigned pierwsze[300] = { 1, 3 };
unsigned iloscPierwszych = 1;
//funkjca wyznacza kolejna liczbe pierwsza
unsigned nastepnaPierwsza()
{
unsigned i;
//sprawdzamy kolejne liczby nieparzyste wieksze od ostatniej liczby pierwszej
for(unsigned liczba = pierwsze[iloscPierwszych - 1] + 2;; liczba += 2)
{
bool czy_pierwsza = true;
unsigned root = sqrt((double)liczba);
//sprawdzamy, czy liczba dzieli sie bez reszty przez ktorakolwiek z wyznaczonych
//liczb pierwszych z pominieciem dwojki bo wiemy ze liczba jest nieparzysta
//sprawdzane sa liczby pierwsze mniejsze od pierwiastka kwadratowego z liczby
for(i = 1; pierwsze[i] <= root; i++)
{
//jesli traimy na czynnik pierwszy to przerywamy
//petle zaznaczajac, ze liczba nie jest pierwsza
if((liczba % pierwsze[i]) == 0) { czy_pierwsza = false; break; }
}
//jesli liczba jest liczba pierwsza to dopisujemy ja do tablicy i przerywamy funkjce
if(czy_pierwsza)
{
pierwsze[iloscPierwszych] = liczba;
iloscPierwszych++;
return liczba;
}
}
}
int main(int argc, char* argv[])
{
unsigned liczba, pierwsza = 2;
for(;;)
{
cout << "Podaj dowolna liczbe naturalna mniejsza od 1000: ";
cin >> liczba;
if(liczba < 1000) break;
cout << "Podana liczba jest zbyt duza" << endl;
}
cout << "Kolejne czynniki pierwsze podanej liczby to:" << endl;
//bedziemy dzielic liczbe przez jej czynniki pierwsze, az stanie sie jedynka
while(liczba > 1)
{
//dopuki rozkladana liczba dzieli sie przez liczbe pierwsza
if((liczba % pierwsza) == 0)
{
cout << pierwsza << ", "; //wypisujemy czynnik pierwszy
liczba /= pierwsza; //i dzielimy przez niego liczbe
}
//jesli rozkladana liczba nie dzieli sie przez liczbe
//pierwsza to wyznaczamy nastepna liczbe pierwsza
else pierwsza = nastepnaPierwsza();
}
cout << endl;
system("PAUSE");
return 0;
}