Skalowanie obrazu (interpolacja, upscaling)

Nie wiem o co dokładnie chodzi, ale podejrzewam próbę wynajdywania koła na nowo.

Podam dla uproszczenia przykład skalowania wiersza (czyli jednowymiarowego odcinka). Potem już sobie można to uogólnić do skalowania dwywymiarowej bitmapy.

Bierzez sobie wiersz lub kolumnę i robisz z tego funkcję y(x)=V gdzie x to numer kolejnego piksela a V to wartość koloru pojedynczego kanału lub para (rg,b) czy (r,g,b,a) jeśli liczysz z przezroczystością (a od alpha), Masz więc osie X i Y, gdzie współrzędne X to kolejne numery elementów w wierszu, zaś Y to te wartości jakie przyjmumuje kolor. Odległości między kolejnymi elementami wiersza przyjmujesz sobie za wartość 1. To znaczy x1-x2=1.

Teraz aby przeskalować sobie taki wiersz musisz po prostu podzielić sobie obszar pomiędzy x0 oraz xN na odpowiednią ilość przedziałów. Właśnie po to przyjmuje się odległość między kolejnymi x skalowanego obrazu by można było trafić między punktami. Np. jeśli trafisz 0,36 jednostek na prawo od punktu x3 to przykładowo liczysz sobie najprymitywniejszą metodą y_poprzeskalowaniu_w_punkcie_którymśtam=y(x3)0,36+y(x4)(1-0,36). Przy pomniejszaniu obrazu punktów tych będzie mniej niż masz w wierszu znanych pikseli(tych z oryginalnego obrazu) przy powiększaniu więcej.

Zamienia się więc problem wartości piksela w problem znajdywania wartości funkcji w danym punkcie w momencie gdy wartości funkcji znane są tylko dla co któregoś punktu, a pomiędzy nimi już musisz w jakiś zorganizowany sposób zgadywać.

Żeby to przerobić na skalowanie wierszy i kolum jednocześnie musisz sobie to przerobić na znajdywanie punktu na dwywymiarowej płaszczyźnie.

Satanistyczny Awatar napisał(a):

Teraz aby przeskalować sobie taki wiersz musisz po prostu podzielić sobie obszar pomiędzy x0 oraz xN na odpowiednią ilość przedziałów. Właśnie po to przyjmuje się odległość między kolejnymi x skalowanego obrazu by można było trafić między punktami. Np. jeśli trafisz 0,36 jednostek na prawo od punktu x3 to przykładowo liczysz sobie najprymitywniejszą metodą y_poprzeskalowaniu_w_punkcie_którymśtam=y(x3)0,36+y(x4)(1-0,36).

To jest zbyt duze uproszczenie. Pomniejszanie nie rozni sie bardzo duzo od powiekszania i da sie napisac kod ktory bedzie dzialal jednoczesnie w obydwu kierunkach, ale w przypadku pomniejszania sensownosc interpolacji miedzy 2 pikselami jest mocno dyskusyjna. Np. piksel wyjsciowy moze byc zmapowany na zakres pikseli wejsciowych od 3.2 do 17.9. Owszem, mozna to policzyc inaczej, uzyskac pojedyncza wartosc reprezentujaca zakres i interpolowac 2 piksele, ale wybranie 2 pikseli z kilkunastu raczej nie da lepszych wynikow niz np. wybranie pojedynczego (np. INTER_NEAREST z opencv). W praktyce calkiem przyzwoite rezultaty daje policzenie sredniej wazonej (trzeba uwzglednic ulamkowe czesci pikseli na brzegach) dla wszystkich pikseli zrodlowych ktore odpowiadaja pikselowi docelowemu (czyli odpowiednik INTER_AREA z opencv).

Jedziesz jednym algorytmem i możesz sobie skalować szerokość i wysokość indywidualnie i mieć gdzieś czy dany wymiar powiększa, zmniejsza czy nie. Wystarcza? Wystarcza. Chcesz się bawić w mnożenie przypadków szczególnych? Droga wolna.

Najlepszą z metod skalowania jest chyba FFT.

1. robimy FFT obrazu, otrzymujemy tablicę współczynników o wymiarach obrazu

2. skalowanie:
   a. przy zmniejszaniu obrazu nic nie robimy, po prostu obcinamy tablicę, czyli odrzucamy część wsp.
   b. przy powiększaniu: należy dołączyć więcej wsp. do tablicy - jak?
   To jest w zasadzie dowolne, najprościej wyzerować, ale można także coś tam wpisywać... eksperymentalnie;
   warunkiem jest tu chyba, że te współczynniki powinny maleć z indeksem - im dalej tym mniejszy..

3. robimy odwrotną FFT.

Crow napisał(a):

Witam.

Staram się sklecić w miarę wydajny ale też szybki algorytm do skalowania bitmap.

W przypadku powiększania (upscaling) mój wybór padł na interpolację dwuliniową (bilinear), bo po prostu daje niezłe efekty niewielkim kosztem. Nie aż tak dobre jak bicubic, ale przy tym nie jest aż tak wymagająca obliczeniowo. Wydaję mi się, że wszystko robię dobrze, ale jedna rzecz nie daje mi spokoju, więc wyjaśnię po krótce o co chodzi (w przykładzie posłużę się "obrazem" 1D, złożonym z poziomej linii - tak dla ułatwienia).

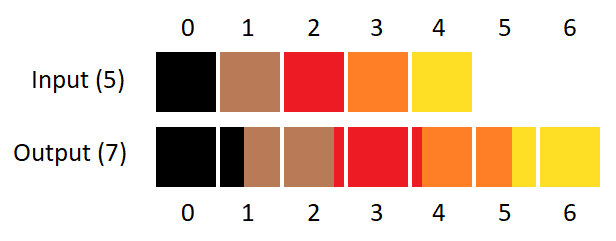
Załóżmy, że mam obraz o szerokości 5, a chciałbym go przeskalować do szerokości 7. Najpierw muszę sobie wyliczyć współrzędne nowych pikseli względem tych pierwotnych.

R = nowa wielkość / oryginalna wielkość = 5/7 = 0,7142
Współrzędna X piksela z obrazu końcowego na obrazie pierwotnym = Współrzędna X piksela obrazu końcowego * R

Czyli kolejno:

X(0) = 0 * R = 0 (kopia piksela 0 z obrazu pierwotnego)
X(1) = 1 * R = 0,7142 (sub-piksel interpolowany pomiędzy pikselem 0 i 1)
X(2) = 2 * R = 1,4284 (sub-piksel interpolowany pomiędzy pikselem 1 i 2)
X(3) = 3 * R = 2,1426 (sub-piksel interpolowany pomiędzy pikselem 2 i 3)
X(4) = 4 * R = 2,8568 (sub-piksel interpolowany pomiędzy pikselem 2 i 3)
X(5) = 5 * R = 3,571 (sub-piksel interpolowany pomiędzy pikselem 3 i 4)
X(6) = 6 * R = 4,2852 (sub-piksel interpolowany pomiędzy pikselem 4 i 5)

Z powyższego wychodzi, że pierwszy piksel końcowego obrazu zawsze jest po prostu kopią pierwszego piksela z obrazu pierwotnego (bo cokolwiek pomnożone przez zero, zawsze da zero), natomiast wszystkie inne piksele są sub-pikselami leżącymi gdzieś na granicy dwóch pikseli pierwotnego obrazu. Tak powinno być? To niby nic wielkiego ale jakoś mi ten pierwszy piksel nie pasuje.

Bo to jest marna metoda.

Należy wyliczać średnią z... fragmentów obrazu, znaczy: całkować to, hihi!

W przypadku zmniejszania o 2 jest to proste:
new_color[i,j] = średnia z 4: 2x2 pikseli = (c[2i, 2j] + c[2i+1, 2j] + c[2i, 2j+1] + c[2i+1, 2j+1]) / 4

I. w przypadku skali niecałkowitej, np. 1/2.5, robimy podobnie: te skrajne dodajemy z wagą 0.5, a potem dzielimy sumę przez 2.5^2 = 6.25.

II. przy powiększaniu można stosować te... interpolacje.

@Crow: pytanie czego oczekujesz od swojego algorytmu. Algorytm, który przedstawiłeś to jakaś odmiana nearest neighbour interpolation, czyli znajdujesz sobie, który uważasz za bazowy, potem wyznaczasz jego sąsiadów, potem sąsiadów sąsiadów itp. Algorytmy z tej grupy są wydajne, natomiast ich słabością jest właśnie sytuacja w której masz duży kontrast pomiędzy pikselami sąsiadującymi z sobą (np. jest szeroka na jeden piksel linia biała, potem niebieska, potem czerwona itp. itd.).

Tutaj masz listę rodzin algorytmów do upscalingu: https://en.wikipedia.org/wiki[...]y_of_image_scaling_algorithms
A tutaj masz zbiór ich implementacji wykorzystywanych w emulacji: https://en.wikipedia.org/wiki/Pixel-art_scaling_algorithms

Crow napisał(a):

Z powyższego wychodzi, że pierwszy piksel końcowego obrazu zawsze jest po prostu kopią pierwszego piksela z obrazu pierwotnego (bo cokolwiek pomnożone przez zero, zawsze da zero), natomiast wszystkie inne piksele są sub-pikselami leżącymi gdzieś na granicy dwóch pikseli pierwotnego obrazu. Tak powinno być?

Tak powinno być, dlatego że szerokość piksela wejściowego jest mniejsza od wyjściowego. Najlepiej pokaże to obrazek:

Jak widać, kolor pierwszego piksela pozostaje bez zmian, drugiego jest mieszanką pierwszego i drugiego, trzeciego jest mieszanką trzeciego i czwartego. Czwarty pozostaje bez zmian, kolejne są mieszankami, a ostatni też pozostaje bez zmian. Kolory pikseli brzegowych ulegną zmianie tylko w przypadku skalowania w dół oraz gdy sąsiadujące z nimi piksele mają inne kolory.

@Crow: do własnych zastosowań wykorzystuję algorytm Pana Davida E. Dirkse — A Bitmap Resize Algorithm, ostatnio na potrzeby Richtrisa, do skalowania zawartości stosu. Pełen opis algorytmu z rysunkami oraz kod źródłowy testowego projektu dla Delphi znajdziesz na jego stronie (u góry są przyciski do pobrania źródeł oraz binarki). Kod co prawda brzydki (wymaga sformatowania), ale za to jest wystarczająco efektywny i daje bardzo ładne rezultaty.

Demówka dołączona do źródeł mierzy czas skalowania i podaje wynik w mikrosekundach.

@furious programming:

A ten algorytm nie ma przypadkiem problemu, o którym wspominał @superdurszlak?

Załóżmy, że chcę przeskalować w dół z 7 do 5. Zgodnie z tym algorytmem powinienem to zrobić w ten sposób:

float F = 7/5 = 1.4

A potem:

0 * F = 0
1 * F = 1.4
2 * F = 2.8
3 * F = 4.2
4 * F = 5.6

Czyli mamy nierówność, zerowy piksel zostaje skopiowany, ale już ostatni stanowi mieszankę 5 i 6 piksela źródłowego. Drugi minus dostrzegam taki, że do skalowania pikseli i tak jest potrzebne 1/F czyli trzeba wykonać dodatkowe dzielenie.

Ja to rozwiązałem podobnie, ale (chyba) lepiej, bo z mniejszą ilość mnożenia i dzielenia. Tutaj przykład funkcji do skalowania w górę w pionie:

void Image::ScaleVerticalUp(int iHeight)
{
    int const NewSize = Data.Width * iHeight;
    Pixel* Output = new Pixel[NewSize]; 
    //Pixel to struktura stanowiąca maskę bajtową dla integera, z którego zbudowany jest bufor obrazka źródłowego { unsigned char B, G, R, A }

    memset(Output, 0, NewSize * sizeof(Output));

    //Data.Bits to bufor zawierający piksele obrazka źródłowego w formie jednowymiarowej tablicy integerów
    //Data.Width i Data.Height to wymiary obrazka źródłowego, a Data.Size to ilość jego wszystkich pikseli (Width * Height)

    float const Ratio = (static_cast<float>(Data.Height - 1) / static_cast<float>(iHeight - 1)) * 0.9999f, Dec = 1.0f - Ratio; 
    //tutaj zastosowałem metodę zaproponowaną przez durszlaka, oraz tą z algorytmu podlinkowanego przez ciebie :).

    float Value = 0.0f, Slice = 1.0f;
    Pixel* In_T = reinterpret_cast<Pixel*>(Data.Bits), * In_B = In_T + Data.Width, * Out = Output, * RowEnd = &Output[Data.Width];
    Pixel* const ColumnEnd = &Output[NewSize]; 

    for (; Out < ColumnEnd; RowEnd += Data.Width)
    {
        for (; Out < RowEnd; Out++, In_T++, In_B++)
        {
            Out->R = (In_T->R * Slice) + (In_B->R * Value);
            Out->G = (In_T->G * Slice) + (In_B->G * Value);
            Out->B = (In_T->B * Slice) + (In_B->B * Value);
        }

        if (static_cast<int>(Value + Ratio)) Value -= Dec;
        else
        {
            Value += Ratio;
            In_T -= Data.Width;
            In_B -= Data.Width;
        }

        Slice = 1 - Value;
    }

    delete[] Data.Bits;
    Data.Bits = reinterpret_cast<int*>(Output);
    Data.Height = iHeight;
    Data.Size = NewSize;
}

Problem miałem już w zasadzie tylko z zaokrąglaniem floatów, bo w testach mi wyszło, że dla niektórych wartości (długości i szerokości obrazka) 10 razy działało dobrze, a potem raz wywalało błąd, bo za każdym razem floaty były zaokrąglane trochę inaczej i czasem wyłaziło mi za bufor... No ale zastosowałem ten trick z przemnożeniem przez 0.9999 i pomogło. Czyli jednak się przydało, dzięki ;).

Wydaje mi się, że jeśli skalujesz w dół to wynikowy piksel może być średnią z więcej niż dwóch wejściowych pikseli. Dla przykładu jeśli skalujesz 10x w dół (w jednym wymiarze) to wynikowy piksel jest średnią z 10 pikseli na wejściu.

O ile dobrze rozumiem to jeśli odwrócimy proces opisany przez @furious programming

i będziemy skalować z 7 pikseli do 5 to okaże się, że środkowy wynikowy piksel będzie średnią ważoną z 3 wejściowych pikseli.

Crow napisał(a):

@furious programming:

A ten algorytm nie ma przypadkiem problemu, o którym wspominał @superdurszlak?

Załóżmy, że chcę przeskalować w dół z 7 do 5. Zgodnie z tym algorytmem powinienem to zrobić w ten sposób:

float F = 7/5 = 1.4

A potem:

0 * F = 0
1 * F = 1.4
2 * F = 2.8
3 * F = 4.2
4 * F = 5.6

Wyznaczyłeś więc krawędzie pikseli tak jak tutaj jest to opisane: http://entropymine.com/imageworsener/matching/
Wynikowe piksele to średnia ważona z tego co jest pomiędzy pikselami, a więc:

• pix_out_0 = (pix_in_0 * 1 + pix_in_1 * 0.4) / 1.4
• pix_out_1 = (pix_in_1 * 0.6 + pix_in_2 * 0.8) / 1.4
• pix_out_2 = (pix_in_2 * 0.2 + pix_in_3 * 1 + pix_in_4 * 0.2) / 1.4 <- uwaga: tutaj uśredniamy 3 piksele, mimo iż skalowanie to tylko 1.4x w dół!
• pix_out_3 = (pix_in_4 * 0.8 + pix_in_5 * 0.6) / 1.4
• pix_out_4 = (pix_in_5 * 0.4 + pix_in_6 * 1) / 1.4

Proces jest więc symetryczny, a każdy piksel ma taki sam wpływ na wynik. Suma nieznormalizowanych wag (trzeba podzielić przez 1.4) dla każdego piksela wejściowego jest równa:

• pix_in_0 = 1
• pix_in_1 = 0.4 + 0.6 = 1
• pix_in_2 = 0.8 + 0.2 = 1
• pix_in_3 = 1
• pix_in_4 = 0.2 + 0.8 = 1
• pix_in_5 = 0.6 + 0.4 =1
• pix_in_6 = 1