Oto jak wygląda problem:
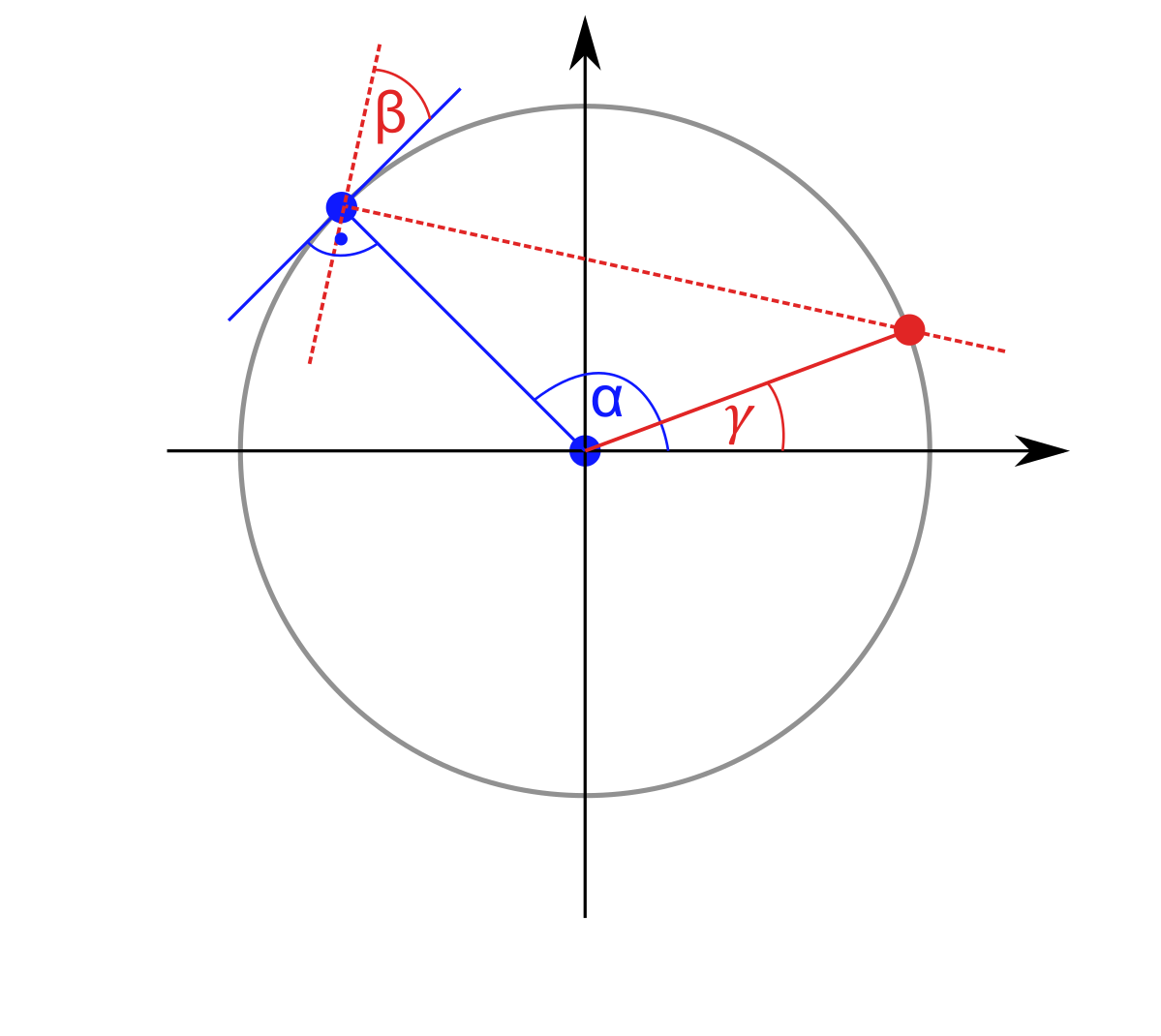
Dany jest kąt alfa w zakresie <0; 360> oraz kąt beta w zakresie <-40; 40>.
Kąt alfa wyznacza prostą prostopadłą do stycznej. Kąt beta określa odchylenie tej stycznej.
Kąt gamma powinien wyznaczać "punkt przecięcia" okręgu z prostą prostopadłą do odchylonej stycznej.
Jak znaleźć kąt gamma?