Określenie parzystości liczby kombinacji w zbiorze liczb całkowitych

Spędziłem kilka godzin nad zadaniem Simple Fun #119: Sub Sets Parity. Jeśli ktoś lubi zadania algorytmiczne i chciałby zrobić to ciekawe zadanie, to ostrzegam, że ten post jest spojlerem.

Wzór na liczbę kombinacji:

Pomysły zmieniały mi się od mało wydajnych do maksymalnie (według mnie) zoptymalizowanych:

• obliczanie liczby kombinacji za pomocą wzoru,
• ograniczenie dwóch wyrażeń z silnią z mianownika do jednego i skracanie liczb za pomocą wyszukiwania największych wspólnych wielokrotności,
• iteracja przez wszystkie możliwości za pomocą rekurencji i negowanie bitu parzystości bez zapamiętywania ilości kombinacji,
• rezygnacja z kolekcji, wykluczenie liczb nieparzystych i wyszukiwanie ilości możliwości podzielenia przez 2 liczb z licznika i z mianownika, a na końcu porównanie tych ilości.

Mój ostateczny poprawny, ale niezaakceptowany kod (z powodu "Execution Timed Out"):

public string SubsetsParity(int n, int k)
{
    var subsetLength = n - k;

    if (k == 1 || subsetLength == 1)
    {
        return (n & 1) == 0 ? "EVEN" : "ODD";
    }

    var twoFactorsCount = 0;
    var subsetValue = 2;

    while (subsetValue <= subsetLength)
    {
        var parityMask = 1;

        while ((subsetValue & parityMask) == 0)
        {
            parityMask <<= 1;
            twoFactorsCount++;
        }

        subsetValue += 2;
    }

    subsetValue = ((k + 1) & 1) == 0 ? k + 1 : k + 2;

    while (subsetValue <= n)
    {
        var parityMask = 1;

        while ((subsetValue & parityMask) == 0)
        {
            if (twoFactorsCount == 0)
            {
                return "EVEN";
            }

            parityMask <<= 1;
            twoFactorsCount--;
        }

        subsetValue += 2;
    }

    return "ODD";
}

Po kilku godzinach otrzymywania "Out Of Memory" lub "Execution Timed Out" poddałem się i sprawdziłem rozwiązania. Nie zdarza mi się rezygnować w przypadku tego typu zadań, ale tym razem nie miałem już nadziei na jeszcze lepszy pomysł. Wydawało mi się, że jeśli wzór jest skomplikowany, to nie istnieje rozwiązanie o złożoności obliczeniowej O(1). Największe zdziwienie, że takie rozwiązanie jest możliwe:

public string SubsetsParity(int n, int k){
    return (k & (n-k)) != 0 ? "EVEN" : "ODD";
}

Czy ktoś z was wie, dlaczego to rozwiązanie działa? Robiliście to zadanie i macie swoje rozwiązania, które zostały zaakceptowane?

Zastanówmy się, tak z matematycznego punktu widzenia, kiedy iloczyn k liczb jest parzysty? Otóż: kiedy przynajmniej jeden z czynników jest parzysty. Nic więcej, wystarczy że jeden czynnik jest parzysty i cały iloczyn będzie parzysty. Co więcej w silniach co drugi element jest parzysty.

Oni w tym śmiesznym sposobie chcą sprawdzić ile parzystych czynników jest w mianowniku. W liczniku wiadomo że jest ich n/2 (-1) w zależności od tego czy n jest parzyste czy nie, bo co drugi czynnik jest parzysty.
Trzeba by to sobie udowodnić, ale zgaduje ze te parzyste elementy ładnie się "znoszą", a przynajmniej ich parzystość się tutaj znosi, więc jeśli licznik i mianownik mają tyle samo parzystych wyrazów, to wynik będzie nieparzysty, ale jeśli mianownik ma parzystych wyrazów mniej, to wynik będzie parzysty

Shalom, nawet jeśli ilość parzystych czynników w liczniku i w mianowniku jest taka sama, to niekoniecznie po skróceniu ich wyniki w liczniku i w mianowniku będą nieparzyste - w tym przypadku to nie jest reguła. Trzeba jeszcze policzyć, przez ile dwójek dzieli się każdy z czynników i dopiero wtedy porównać ich sumy.

Ale tak się zastanawiam, co jest z tą sztuczką w najprostszym rozwiązaniu. Jeśli np. n = 10 i k = 3, to wynikiem będzie (8 * 9 * 10) / (1 * 2 * 3). Oni sprawdzają, czy liczby 3 i 7 mają jakieś wspólne bity i tylko od tego zależy, czy rozwiązanie będzie parzyste, czy nieparzyste. Dla mnie tylko to jest niezrozumiałe.

Nie no nie sprawdzają żadnych wspólnych bitów :D Sprawdzają tylko ostatni bit, który mówi czy liczba jest parzysta czy nie ;) Jeśli ostatni bit jest 1 to liczba jest nieparzysta, a jeśli 0 to parzysta. Oni sprawdzają tylko czy k oraz n-k są jednocześnie parzyste czy nie są.

Jeśli chodzi o samo skrócenie, to fakt że liczba kombinacji nigdy nie jest ułamkiem, sugeruje że jednak tam się zawsze ładnie skraca ;)

Shalom napisał(a):

Nie no nie sprawdzają żadnych wspólnych bitów :D Sprawdzają tylko ostatni bit, który mówi czy liczba jest parzysta czy nie ;) Jeśli ostatni bit jest 1 to liczba jest nieparzysta, a jeśli 0 to parzysta. Oni sprawdzają tylko czy k oraz n-k są jednocześnie parzyste czy nie są.

Zauważ, że takie sprawdzenie np. dla liczb dwójkowych 100 i 101 da wynik różny od zera i np. dla 100 i 110 też da różny od zera, ale parzystości w pierwszym przypadku są różne, a w drugim takie same.

Shalom napisał(a):

Jeśli chodzi o samo skrócenie, to fakt że liczba kombinacji nigdy nie jest ułamkiem, sugeruje że jednak tam się zawsze ładnie skraca ;)

Ale tutaj nie chodzi o liczby pierwsze i złożone, tylko o parzyste i nieparzyste. Nieparzyste z parzystymi tak samo ładnie się skracają jak nieparzyste z nieparzystymi, np. dla takich różnych kombinacji parzystości i nieparzystości wynik zawsze jest całkowity: 15 / 3, 8 / 2, 12 / 3, 10 / 5.

Shalom napisał(a):

Nie no nie sprawdzają żadnych wspólnych bitów :D Sprawdzają tylko ostatni bit, który mówi czy liczba jest parzysta czy nie ;) Jeśli ostatni bit jest 1 to liczba jest nieparzysta, a jeśli 0 to parzysta. Oni sprawdzają tylko czy k oraz n-k są jednocześnie parzyste czy nie są.

To tak nie działa. Przykładowe przypadki:

Jeśli obie liczby są nieparzyste, to wyrażenie zawsze będzie prawdziwe, ale prawdziwość wyrażenia nie oznacza, że obie liczby są nieparzyste. Więc prawdziwość wyrażenia oznacza, że jest szansa na to, że te obie liczby są nieparzyste, a nieprawdziwość pokazuje, że można mieć pewność, że obie liczby nie są jednocześnie nieparzyste.

Hm dobra faktycznie założyłem że tam jest jakieś &1 jeszcze, a nie ma, więc w sumie ten warunek sprawdza czy liczby k oraz n-k mają jakikolwiek wspólny zapalony bit.
A wynika to chyba z takiego twierdzenia: https://en.wikipedia.org/wiki/Lucas's_theorem
Tutaj jest przykład dla mod 3 -> https://math.stackexchange.com/questions/95476/lucas-theorem-for-combinatorics ale idea jest dokładnie taka sama

To by wszystko wyjaśniało. Dzisiaj już tego nie ogarnę, ale jutro spróbuję coś z tego zrozumieć.

To zdanie z podanego przez Ciebie artykułu na wikipedii najwięcej mi mówi:

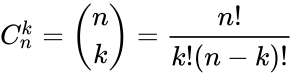
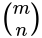A binomial coefficient is divisible by a prime p if and only if at least one of the base p digits of n is greater than the corresponding digit of m.

Dzięki temu mogę osiągnąć taki kod, który przechodzi bez problemu:

public string SubsetsParity(int n, int k)
{
    while (k != 0)
    {
        if ((n & 1) == 0 && (k & 1) == 1)
        {
            return "EVEN";
        }
         
        k >>= 1;
        n >>= 1;
    }
      
    return "ODD";
}

Widzę, że jest taka zależność dla bitów na tej samej pozycji: jeśli bit w n nie jest ustawiony, ale w k jest ustawiony, to w n - k tylko dla takiego przypadku też jest ustawiony, dlatego to sprawdzenie (k & (n - k)) != 0 działa.