Witam mam pewien problem z zadaniem z algorytmów . Nie chodzi mi to napisanie kodu czy czegoś w tym rodzaju , po prostu nie rozumiem jak dla zadanych danych wejściowych mogą wyjść takie dane wyjściowe. Jeżeli był by ktoś taki dobry i napisał jak zrozumieć te zadanie to byłbym wdzięczny ;_)
W duzym nowym osiedlu planowane jest postawienie transformatorów obsługujacych
osiedlowa siec przesyłu energii elektrycznej. Ustalono ju? mo?liwe do zrealizowania
lokalizacje transformatorów i projekt linii przesyłu łaczacych te transformatory. Nalezy
jeszcze jednak, ze zbioru ustalonych lokalizacji, wybrac te, które zapewni? przesył energii
kazda linia sieci. Przy czym nalezy zadbac o to, aby wybranych lokalizacji
zapewniajacych przesył na ka?dym łaczu sieci było jak najmniej.
Zaproponuj algorytm, który na podstawie grafu sieci ustali najmniejszy podzbiór
lokalizacji transformatorów, zapewniaj?cy przesył energii w kazdym łaczu sieci.
Plik wejsciowy: Plik tekstowy o nazwie Siec_nazwisko_grupa_in.txt ma nastepujacy
format: W pierwszej linijce pliku znajduje sie liczba całkowita n (0<n?200) okreslajaca
liczba transformatorów. W kolejnych n linijkach pliku znajduje sie co najwyzej n-1 liczb
oddzielonych pojedyncza spacja i oznaczajacych linie przesyłu obsługiwane przez dany
transformator. W i -tej linijce znajduje sie numery transformatorów, z którymi jest
połaczony liniami przesyłu transformator o numerze i.
Plik wyjsciowy: Plik tekstowy o nazwie Siec_nazwisko_grupa_out.txt ma nastepujacy
format: W pierwszej linijce pliku znajduje sie jedna liczba całkowita min oznaczajaca
rozmiar podzbioru wybranych lokalizacji transformatorów. W drugiej linijce znajduje sie
min liczb całkowitych oddzielonych pojedyncza spacja i oznaczajacych numery
lokalizacji, które nalezy do tego minimalnego podzbioru.
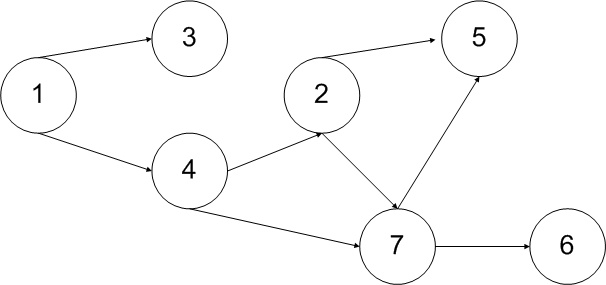
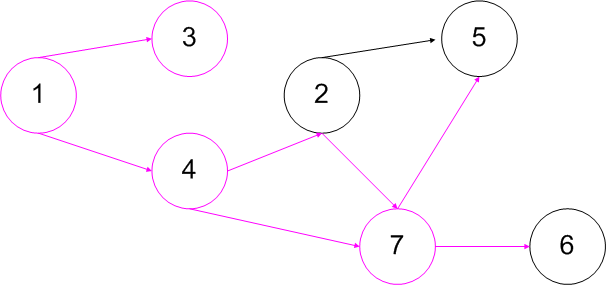
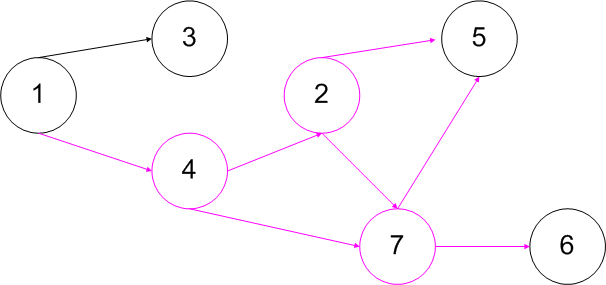
Przykład
Siec_nazwisko_grupa_in.txt
7
3 4
4 5 7
1
1 2 7
2 7
7
2 4 5 6
Siec_nazwisko_grupa_out.txt
3
2 4 7
Jak bym nie patrzył na to zadanie to zawsze wychodzi mi że dane wyjsciowe to 1 4 7.
Z góry dziękuje za wszystkie odpowiedzi ;-)