Jak obliczyć tę sumę praktycznie i numerycznie?
Wynik to podobno: 1+1+1+1+... = -1/2.
Jak obliczyć tę sumę praktycznie i numerycznie?
Wynik to podobno: 1+1+1+1+... = -1/2.
Wiesz że dzwonią ale nie wiesz w którym kościele i pomieszałeś dwa ciągi.
https://en.wikipedia.org/wiki/Grandi's_series
https://en.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_⋯
Polecam:
1-1+1-1... = 1/2
1+2+3+4+5+... = -1/12
Takie coś naprzemienne - plusy i minusy, to bez problemu ręcznie nawet małpoludy obliczają.
np.:
s = 1-1+1-1+...
no i co to za problem?
wystarczy tak chlapnąć:
s = 1-1+1-1+... = 1 - (1-1+1-1+ ...) = 1 -s;
tym samym:
2s = 1, czyli s = 1/2
I podobnie robimy takie coś:
s = 1 - 2 + 3 - 4 + ... = ?
a zresztą to jest to samo, bowiem: 1/(1+x) = 1 - x + x2 - x3 + ...
i po zróżniczkowaniu da od razu mamy: -1 + 2x - 3x2 + 4x3 - ...
co już nietrudno wyliczyć.
Shalom napisał(a):
Wiesz że dzwonią ale nie wiesz w którym kościele i pomieszałeś dwa ciągi.
https://en.wikipedia.org/wiki/Grandi's_series
https://en.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_⋯
Chyba chciałeś powiedzieć że Ty pomieszałeś... no ale to też ci się pomieszało... :)
Może tak to można załatwić- obie sumy naraz:
a = 1+2+3+... oraz b = 1+1+1+...
zatem:
a-b = (1+2+3+...) - (1+1+1+...) = 0+1+2+3+... = s
ale zarazem:
a+b = (1+2+3+...) + (1+1+1+...) = 2+3+... = s-1
sumując to stronami:
2a = 2s-1, zatem: a = s - 1/2, i nadal nic nie wiadomo...
no, ale za to odejmując otrzymamy:
2b = -1, czyli: b = -1/2;
i całkiem prawidłowo!
Ciekawe co z tym a - co tu wyjdzie?
b = -1/2, zatem:
a+1/2 = s i a-1/2 = s-1
a-s = -1/2 i a-s = -1/2
no, czyli to nadal nam nie rozstrzyga czym jest to a... bardzo zabawne. :)
a = 1+2+3+4+5+... = -1/12
ShookTea napisał(a):
a = 1+2+3+4+5+... = -1/12
No, chyba można tak:
1+2+3+4... - (1-2+3-4+...) = 0+4+8+12+... = 4(1+2+3+...) = 4a
mając już: c = 1-2+3-4+... = 1/4
wtedy otrzymamy:
a - 1/4 = 4a => 3a = -1/4 => a = -1/12
tylko że w tym filmie i tak nie wyliczyli tej mojej sumki: 1+1+1+... = -1/2
A może jeszcze coś innego, np. takie coś:
1+3+5+7+ ... = ?
same nieparzyste;
a więc i parzyste wypada od razu: 2+4+6+... = ?
@tłusty łysy byk:
Mi wyszło co innego:
s = 1 + 2 + 3 + ... = -1/ 12
s1 = 1 + 1 + 1 + ... = ?
s = 1 + 3 + 5 + ...
+ 2 + 4 + 6 + ...
= 1 + 1 + 1 + ...
+ 0 + 2 + 4 + ...
+ 2 + 4 + 6 + ...
= s1 + 4 * s
s = s1 + 4 * s
s1 = -3 * s
s1 = -3 * (-1/ 12) = 1/ 4
Idąc dalej:
s1 = 1 + 1 + 1 + ... = 1/ 4
s1 = 1 + 1 + 1 + ...
= 1 + s1
1/ 4 = 1 + 1/ 4
0 = 1
I jeszcze dalej:
0 = 1
4 = 5
2 + 2 = 5
et voilà!
Suma 1+1+1+... albo 1+2+3+4... nie może wynosić -1/12 ani -1/2 ani nic podobnego, bo każdy kolejny składnik powoduje że suma jest WIĘKSZA, więc jakim cudem miałaby się stać nagle mniejsza a co dopiero ujemna.
@Azarien już trzeci raz linkuję:
Zauważ, że facet pokazuje w 0:44 książkę o teorii strun z tą sumą. No i później tłumaczy, skąd ten wynik.
Ogólnie, matematyka jest przecież pełna takich niby-to sprzeczności. Wiadomo przecież, że na przykład zawsze
a - 1 < a
Ale przecież ∞ - 1 jest nadal równe ∞.
PS. Tak, tak, tak, nieskończoność nie jest liczbą. To tylko taki przykład.
Wibowit napisał(a):
@tłusty łysy byk:
Mi wyszło co innego:
s = 1 + 2 + 3 + ... = -1/ 12
s1 = 1 + 1 + 1 + ... = ?
s = 1 + 3 + 5 + ...
2 + 4 + 6 + ...
= 1 + 1 + 1 + ...</li>
0 + 2 + 4 + ...</li>
2 + 4 + 6 + ...
= s1 + 4 * s</li>
</ul>
s = s1 + 4 * s
s1 = -3 * s
s1 = -3 * (-1/ 12) = 1/ 4
>
>
> Idąc dalej:
> <code>s1 = 1 + 1 + 1 + ... = 1/ 4
s1 = 1 + 1 + 1 + ...
= 1 + s1
1/ 4 = 1 + 1/ 4
0 = 1
I jeszcze dalej:
0 = 1
4 = 5
2 + 2 = 5
>
> et voilà!
Oczywiście że tak jest, znaczy sumy tego typu - szeregi rozbieżne, mogą być dowolne,
tz. gdy założysz np. że 1+1+1+ ... = 7, no to możesz to potem wykazać formalnie.
Niemniej te liczby: 1+1+1+... = -1/2, itd. są tu jakoś szczególne w tej... matematyce absurdalnej. :)
One mają zwykle jakiś tam sens fizyczny, np.:
1-1+1-1+ ... = 1/2
choć granica szeregu nie istnieje - zgodnie z definicjami.
Ale widać co ta 1/2 tu reprezentuje: średnia 0 i 1, bowiem tak skacze suma częściowa:
1 = 1,
1-1 = 0
1-1+1 = 1
...
itd.
i średnio jest właśnie: 1/2.
Gorzej jest z tymi ujemnymi, typu: 1+1+1+... = -1/2
dlaczego akurat tyle, jaki to ma sens w fizyce?
Znacznie trudniej wyczuć... no ale coś w tym jest.
Azarien napisał(a):
Suma 1+1+1+... albo 1+2+3+4... nie może wynosić -1/12 ani -1/2 ani nic podobnego, bo każdy kolejny składnik powoduje że suma jest WIĘKSZA, więc jakim cudem miałaby się stać nagle mniejsza a co dopiero ujemna.
A to akurat pikuś... są znane szeregi liczb dodatnich, których suma jest urojona!
Wyobrażasz to sobie?
Wygląda to tak...
albo zresztą sam sobie to oblicz, tz. podaj szereg liczb całkowitych, którego suma będzie urojona, np. dokładnie i. :)
A może takie jest uzasadnienie dla tych ujemnych sum,
powracając od razu do mojego pytania:
1+1+1+... = -1/2
to akurat jest dość kłopotliwe... no, ale weźmy inny szereg:
1 + 2 + 4 + 8 + ... = -1
też śmiesznie, no ale gdy sumujemy to na jakimś hiper pececie, wówczas właśnie tak wyjdzie,
ponieważ binarnie byłoby to:
1 + 10 + 100 + ... = 111111111111111... = -1; dokładnie, w reprezentacji ze znakiem... :)
Halo halo, bo widze, że tu herezje zaczynają się tworzyć. Ciągów o nieistniejących granicach nie można w ten sposób dodawać ze sobą. Kropka. Mogę pokazać, że 1+1+1+...+1 jest dowolną liczbą. Czy jest tak naprawdę? Nie, nie jest. Suma takiego ciągu jest nieokreślona, kropka. Natomiast wynik -1/12 jest często wykorzystywany w fizyce.
@ShookTea "@Azarien już trzeci raz linkuję:
Zauważ, że facet pokazuje w 0:44 książkę o teorii strun z tą sumą. No i później tłumaczy, skąd ten wynik.
Ogólnie, matematyka jest przecież pełna takich niby-to sprzeczności. Wiadomo przecież, że na przykład zawsze
a - 1 < a
Ale przecież ∞ - 1 jest nadal równe ∞.
PS. Tak, tak, tak, nieskończoność nie jest liczbą. To tylko taki przykład. "
Bzdury Pan pleciesz. Nierówność jest prawdziwa w ciele liczb
(i kilku innych). Powiesz mi, że
? Nie, chociażby dlatego, że nie jest liczbą. Nieskończoność sama w sobie jest elementem rozszerzonego zbioru
, czyli zbioru
w którym Twoja nierówność nie jest spełniona.
BTW, jakb ktoś mi wytłumaczył, jak latexa tutaj używać, to byłbym wdzięczny.
Natomiast wynik -1/12 jest często wykorzystywany w fizyce.
Zauważ, że facet pokazuje w 0:44 książkę o teorii strun z tą sumą. No i później tłumaczy, skąd ten wynik.
ZTCW to ten wynik jest wykorzystywany tylko w teorii strun, a sama teoria strun jest jak na razie niepotwierdzona i nie przynosi żadnych korzyści.
Wibowit napisał(a):
Natomiast wynik -1/12 jest często wykorzystywany w fizyce.
Zauważ, że facet pokazuje w 0:44 książkę o teorii strun z tą sumą. No i później tłumaczy, skąd ten wynik.
ZTCW to ten wynik jest wykorzystywany tylko w teorii strun, a sama teoria strun jest jak na razie niepotwierdzona i nie przynosi żadnych korzyści.
Teoria strun, czy raczej pseudoteoria, nie specjalnie ma coś tu do powiedzenia.
Takie rozbieżne sumy to domena fizyki kwantowej - tej maded by Feynman.
Przykładowo: masa własna elektronu wychodzi nieskończona, wedle klasycznego rachunku
(dobrze znany paradoks z elektrodynamiki..),
no ale my jednak wiemy, że ona jest skończona, bo wynosi około: 1e-30 kg, zaledwie.
Zatem co pan Feynman na to?
Ano, on właśnie taki szereg rozbieżny (faktycznie była to całka) 'przeliczył' w taki właśnie sposób,
żeby suma była skończona, no i zgodna zarazem z tym co znamy - mierzymy.
... no i właśnie za to dostał nobla. :)
a = 1+1+1+...+1 = -1/2
1 + (1+1+1+...+1) = 1 + a = 1/2
1/2 = -1/2
to jeż jest zgodne z tym co mierzymy? Skończmy ten bullshit tutaj, naprawde.
Nawet nie trzeba zakładać, że coś jest równe -1/ 2 albo -1/ 12:
s1 = 1 + 1 + 1 + ...
= 1 + s1
s1 = 1 + s1
0 = 1
pingwindyktator napisał(a):
a = 1+1+1+...+1 = -1/2
1 + (1+1+1+...+1) = 1 + a = 1/2
1/2 = -1/2
to jeż jest zgodne z tym co mierzymy? Skończmy ten bullshit tutaj, naprawde.
Błędnie liczysz, a potem się dziwisz...
jeśli chcesz się trzymać twardo zasad, no to musiałbyś tak to zapisać:
a = 1+1+1+...+1 = -1/2 =>
1 + (1+1+1+...) = 1 + (a-1) = -1/2
zatem odkryłeś rewelację typu:
-1/2 = -1/2 :)
Może coś ambitniejszego popróbujecie?
na przykład:
oo! = 1234... = ?
przypominam że: ln(n!) = ln1 + ln2 + ln3 +...+ ln(n); :)
Litości, człowieku. Obie sumy są nieokreślone.
Ale tu herezje w tym wątku lecą ;).
Ogólnie, matematyka jest przecież pełna takich niby-to sprzeczności. Wiadomo przecież, że na przykład zawsze
a - 1 < a
Ale przecież ∞ - 1 jest nadal równe ∞.
W matematyce nie ma żadnych sprzeczności (w rzeczach które sie da udowodnić), jeśli znajdziesz jakąś to cała matematyka runie (bo ze sprzeczności można udowodnić każde zdanie, więc jednocześnie obalisz i udowodnisz wszystkie teorie matematyczne).
Weźmy np. podany przez Ciebie przykład (Wiadomo przecież, że na przykład zawsze a - 1 < a) - co to znaczy zawsze? Dla każdej operacji - i < na dowolnym pierścieniu? To trywialnie nieprawdziwe, więc chciałeś powiedzieć coś konkretniejszego: dla dowolnej liczby rzeczywistej zachodzi a - 1 < a. I to jest prawdziwe, ale nie ma żadnej sprzeczności: ∞ nie jest elementem R.
Dlaczego się akurat tego zdania czepiam: bo w matematyce nie ma się o co kłócić, albo coś jest prawdą (i jest udowodnione), albo coś jest nieprawdą (i jest obalone) (ok, są jeszcze otwarte problemy, ale nie widziałem żeby ludzie się zabijali o to czy P=NP, a widziałem niesamowite wojny czy 0.(9) = 1).
Takie coś naprzemienne - plusy i minusy, to bez problemu ręcznie nawet małpoludy obliczają.
np.:
s = 1-1+1-1+...no i co to za problem?
wystarczy tak chlapnąć:
s = 1-1+1-1+... = 1 - (1-1+1-1+ ...) = 1 -s;tym samym:
2s = 1, czyli s = 1/2
Nie wiem, czy to sarkazm? Bo jeśli nie, to nieprawda. Chociażby dlatego że z tej samej logiki wynika że 1 - 1 + 1 - 1 = (1 - 1) + (1 - 1) + ... = 0 (można nawet argumentować sensownie za innymi wartościami, np. 1/2, ale o tym później). Jakby nie patrzeć, suma jednego ciągu nie może jednocześnie mieć dwóch różnych wartości (to by była sprzeczność).
@Azarien już trzeci raz linkuję:
Zauważ, że facet pokazuje w 0:44 książkę o teorii strun z tą sumą. No i później tłumaczy, skąd ten wynik.
No tak, skoro pokazuje ksiażkę o teorii strun z tą sumą to musi być prawdziwa (/sarkazm).
To wideo zrobiło więcej szkody (fud) niż pożytku (szerzenie wiedzy) moim zdaniem. Na pewno jest "ASTOUNDING", ale po numberphile spodziewałbym się wartości merytorycznej a nie nagłówków jak z FAKTu (dla jasności, większość ich filmów jest wartościowa, po prostu ten jeden średnio).
A wracając do ciągu - problem bardzo podobny do tego nieszczęsnego zdania Wiadomo przecież, że na przykład zawsze a - 1 < a, Ale przecież ∞ - 1 jest nadal równe ∞. (odnosiłem sie do niego wcześniej).
Taki sam sens (tzn. brak sensu) ma stwierdzenie Suma 1 + 2 + 3 + ... jest równa [wstaw dowolną liczbę rzeczywistą] - każdy może rozumieć pod tym zdaniem co innego.
Możemy powiedzieć że "suma sekwencji liczb rzeczywistych 1 + 1/2 + 1/4 + 1/8 + ... = 2", bo jest tylko jedna równa ogólnie przyjęta definicja sumy takiego ciągu (spełnia pewne surowe warunki, tzn. wszystkie elementy są nieujemne oraz istnieje stała A taka że suma każdego skończonego podzbioru jest mniejsza od lub równa A). Jeśli chcesz, możesz zawsze zdefiniować sumę takiego ciągu na swój sposób (np. powiedzieć że suma takiego ciągu jest równa 8, z jakiegoś tam powodu), i nie będzie to błąd - ale taka definicja będzie bezużyteczna, więc nikt jej nie będzie używał. Praktyczna jest definicja wg. której ten ciąg sie sumuje do 2.
Do ciągu 1 + 2 + 3 + ... tego nie możemy zastosować (nie ma takiej stałej A, etc). W większości przypadków, taki ciąg uznajemy za niesumowalny, i uznajemy że suma nie istnieje (albo jest rozbieżna do nieskończoności). Ale jeśli się uprzemy, możemy spróbować znaleźć ogólniejszą definicję.
I okazuje sie że są takie definicje. Na przykład https://en.wikipedia.org/wiki/Abel's_summation_formula, https://en.wikipedia.org/wiki/Ces%C3%A0ro_summation, https://en.wikipedia.org/wiki/Borel_summation albo Ramanujan summation. Ostatnia jest szczególnie ciekawa, bo to z niej to nieszczęsne -1/12 wyprowadzono.
Ale rzecz w tym, że w momencie kiedy zaczynamy sumować skończone ciągi, przestajemy mówić o "sumie" (jak "suma liczb 1, 2, 3, 4 jest równa 10) a o konkretnych metodach sumowania.
Więc zdanie "suma ciągu 1 + 2 + 3 + ... = [coś]" jest źle (albo po prostu nieprecyzyjnie) sformułowane, powinno być "Suma Ramanujana obliczona dla ciągu [1, 2, 3, ...] jest równa -1/12".
Powiedzenie, że suma 1 + 2 + 3 + ... wynosi -1/12 to raczej nadużycie (i nie ma co tracić czasu na kłótnie z tym związane), ale faktycznie ta liczba jest z nią w bardzo ciekawy sposób powiązana. Matematykę oraz jej zasady stworzyliśmy w taki sposób by móc za jej pomocą reprezentować zjawiska fizyczne, nawet jeżeli czasami z tych zależności ma wynikać coś pozornie nieintuicyjnego. Bardzo dawno temu za bardzo nieintuicyjne uważano liczby ujemne i uważano, że zepsuje to matematykę, bo miały nie występować w przyrodzie, a dzisiaj za pomocą pierwiastka z -1 drukarka wyostrza zdjęcia przed ich wydrukowaniem i nikt z tego powodu nie podnosi larum. Z kolei suma 1^3 + 2^3 + 3^3 + ... i w taki sam sposób powiązana z nimi wartość 1/120 jest używana np. w wyznaczeniu siły w efekcie Casimira. Co 60 lat temu było strasznie nieintuicyjne, ale dzisiaj potrafimy ją zmierzyć.
Kolejna ciekawostka. Wzór na sumę częściową ciągu arytmetycznego to ((a1+an)*n)/2. Jeżeli użyjemy jej do naszej sumy i zamienimy w funkcję w R to dostaniemy ((1 + x)*x)/2. Jej wykres to:
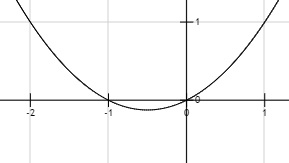
Pole tej małej części pod osią x to właśnie -1/12 :).
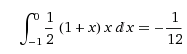
Rev napisał(a):
Powiedzenie, że suma 1 + 2 + 3 + ... wynosi -1/12 to raczej nadużycie (i nie ma co tracić czasu na kłótnie z tym związane), ale faktycznie ta liczba jest z nią w bardzo ciekawy sposób powiązana. Matematykę oraz jej zasady stworzyliśmy w taki sposób by móc za jej pomocą reprezentować zjawiska fizyczne, nawet jeżeli czasami z tych zależności ma wynikać coś pozornie nieintuicyjnego. Bardzo dawno temu za bardzo nieintuicyjne uważano liczby ujemne i uważano, że zepsuje to matematykę, bo miały nie występować w przyrodzie, a dzisiaj za pomocą pierwiastka z -1 drukarka wyostrza zdjęcia przed ich wydrukowaniem i nikt z tego powodu nie podnosi larum. Z kolei suma
1^3 + 2^3 + 3^3 + ...i w taki sam sposób powiązana z nimi wartość 1/120 jest używana np. w wyznaczeniu siły w efekcie Casimira. Co 60 lat temu było strasznie nieintuicyjne, ale dzisiaj potrafimy ją zmierzyć.Kolejna ciekawostka. Wzór na sumę częściową ciągu arytmetycznego to ((a1+an)*n)/2. Jeżeli użyjemy jej do naszej sumy i zamienimy w funkcję w R to dostaniemy ((1 + x)*x)/2. Jej wykres to:
Pole tej małej części pod osią x to właśnie -1/12 :).
Nawet dość ciekawe...
No to może spróbuj pójść nieco dalej, i wytłumacz np. sumę, o której już wspomniałem wcześniej,
tz. jak taka rozbieżna suma rzeczywistych może nam wyskoczyć w zespolone!
W szczególności mamy taki przypadek:
s = 1 + 2 + 6 + 22 + ... = i
Są to tzw. liczby Schrödera, które otrzymujemy jako liczbę możliwych ścieżek w takiej oto matrycy:
http://mathworld.wolfram.com/SchroederNumber.html
wynik s = i jest oczywiście wprost z funkcji tworzącej
(podobnie jak w przypadku 1-1+1+... 1/2, bo tu jest z fun. tworząca: 1 / 1+x),
w której mamy pierwiastek z -1... zatem ta suma może być także równa -i,
zamiast i, ponieważ wiadomo że: sqrt(-1) = +/-i.
Ktoś zamknie ten temat już? - pingwindyktator
A niby jak to sobie wyobrażasz...
sam widzisz że temat jest nieskończony z samej natury. :)
Suma liczb Fibonacciego, tz.:
f = 1 + 1 + 2 + 3 + 5 + 8 + ... = ?
wychodzi tu znowu: f = -1... co było w przypadku:
g = 1 + 2 + 4 + 8 + ... = -1
zatem już chyba widać o co tu chodzi!
Pewnie geometryczne postępy mają 'sumę' = -1 (te liczby Fibonacciego rosną geometrycznie, bo one są w przybliżeniu: Fn = Phi^n, Phi = 1.618... = golden ratio);
no, czyli cały ten cyrk z niby sumowaniem rozbieżnych, to chyba tylko taka klasyfikacja tychże szeregów,
pod względem... szybkości tej rozbieżności, zapewne(?)
Naprzemienne są zawsze dodatnie, np.:
1-1+1-1 +... = 1/2;
potem: 1-2+3-4+ ... = 1/4;
natomiast te tylko dodatnie, jak: 1+1+1+... = -1/2, podobnie 1+2+3+... = -1/12 < 0;
czyli wychodzi jakby mniej, zamiast więcej...
No, ale pomiędzy ujemnymi i dodatnimi jest przecież zero!
Zatem pojawia się pytanie: jaki szereg rozbieżny ma 'sumę' = 0? :)