Metoda prostokątów
mnbvcX
Naszym zadaniem jest obliczyć całkę oznaczoną z funkcji f(x) metodą prostokątów. Polega ona na przybliżeniu pola pod wykresem polami prostokątów:
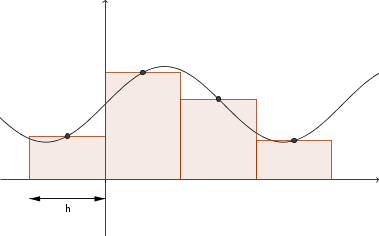
Zauważmy, iż wysokość prostokąta jest równa wartości naszej funkcji w połowie przedziału, zaś szerokość jest identyczna dla każdego czworokąta i jest równa h. Pole takiego prostokąta jest równe:
gdzie p, k to odpowiednio początek i koniec przedziału, w którym mieści się prostokąt.
Ale jak wyznaczyć wartość h? To proste - dzielimy nasz obszar całkowania (górna granica minus dolna granica) na t części i powstaje nam szerokość prostokąta równa h. Czyli po prostu:
Teraz wystarczy policzyć t takich prostokątów. Pierwszy prostokąt zajmuje przedział [a, a+h]; drugi zaczyna się tam, gdzie skończył się pierwszy i ma szerokość h: [a+h, a+2h]; trzeci [a+2h, a+3h] i tak dalej. Jesteśmy więc w stanie policzyć przybliżoną wartość wyrażenia.
Przykład
Liczymy całkę funkcji f(x) = x2 od 0 do 1 (która jest równa dokładnie 1/3).Dzielimy na prostokąty
Dzielimy nasz obszar [0, 1] na 3 równe prostokąty; pierwszy będzie zajmował zakres [0, 1/3], drugi [1/3, 2/3], a trzeci [2/3, 1]. Parametr h jest równy (1-0) / 3 = 1/3.Liczymy pola prostokątów
Prostokąt I jest na obszarze [0, 1/3], czyli środek to 1/6. f(1/6) = 1/36, więc pole równe jest h * f(1/6) = 1/108. Prostokąt II jest na obszarze [1/3, 2/3], środek to 1/2. f(1/2) = 1/4, więc pole jest równe h * f(1/2) = 1/12 Prostokąt III zajmuje obszar [2/3, 1], środek to 5/6. f(5/6) = 25/36, więc pole jest równe h * f(5/6) = 25/108.Sumujemy pola
Sumujemy pola prostokątów: 1/108 + 1/12 + 25/108 = 35/108Błąd pomiaru
Po przybliżeniu trzema prostokątami otrzymujemy pole 35/108, tymczasem pole rzeczywiste wynosi 1/3 = 36/108. Błąd pomiaru wynosi więc 1/108. Gdybyśmy użyli większej liczby prostokątów, otrzymalibyśmy lepsze przybliżenie.Implementacja w C++
Poniższa implementacja dla podanej liczby prostokątów (t) podaje wartość całki f(x) = cos od 0 do 1 i wyznacza błąd pomiaru.#include <cstdio>
#include <cmath>
using namespace std;
int main(){
printf("Poniższy program policzy całkę:\n\n");
printf(" 1\n");
printf(" ==\n");
printf(" |\n");
printf(" | cos(x) dx = 0.841470984807\n");
printf(" |\n");
printf("==\n");
printf(" 0\n\n");
printf("Podaj liczbę prostokątów (t): ");
int t;
scanf("%i", &t);
//min = 0, max = 1, h = (max - min) / t = 1/t
double min = 0.0;
double polozenie, wartosc, calka = 0.0;
double h = 1.0/t;
//wykonujemy t kroków
for(int i = 0; i < t; i++){
//nasz aktualny przedział to [min, min+h];
//potrzebujemy wartości funkcji w połowie przedziału, czyli
//[min + (min+h)] / 2 = min + h/2
polozenie = min + h/2;
//liczymy wartość funkcji cos(x) dla wyliczonego położenia
wartosc = cos(polozenie);
//zwiększamy naszą wartość całki o pole prostokąta.
//Wynosi ono [wartość funkcji] * h.
calka += (wartosc*h);
//aby przedział [min, min+h] był prawidłowy, musimy
//zwiększyć "min" o wartość h - dostaniemy wtedy [min+h, min+2h].
min += h;
}
//wypisujemy naszą całkę
printf("\nWyliczona całka: %.11f\n", calka);
printf("Błąd: %.11f\n", abs(calka-0.841470984807));
}
Błędy pomiaru
Całkowanie numeryczne jest metodą przybliżającą pole. Oznacza to, iż nie podaje dokładnej wartości całki. W poniższej tabeli zawarte są błędy pomiaru w zależności od ilości użytych prostokątów.| Prostokąty | Błąd |
| 1 | 0,03611157708 |
| 3 | 0,00390836104 |
| 10 | 0,00035071520 |
| 100 | 0,00000350614 |
| 250 | 0,00000056098 |
| 1000 | 0,00000003506 |
| 10000 | 0,00000000035 |
Łatwo zauważyć w tym przypadku, że jeśli liczba prostokątów rośnie 10-krotnie, błąd maleje stukrotnie. Należy jednak wziąć pod uwagę, że algorytm dla funkcji z dużą zmiennością może być słabszy.
W Delphi: http://4programmers.net/Delphi/Artykuły/Proste_całkowanie