Całkowanie numeryczne metodą Simpsona
Wstęp
Metoda Simpsona jest bardziej zaawansowaną metodą obliczania całki przez przybliżenie pola pod wykresem, która od metody trapezów różni się stopniem wielomianu, którym przybliżana jest funkcja w poszczególnych przedziałach - o ile w metodzie trapezów wielomian był pierwszego stopnia (f. liniowa) przechodzący przez 2 punkty, to w metodzie Simpsona stosujemy wielomian interpolacyjny drugiego stopnia (parabola) przechodzący przez 3 punkty.
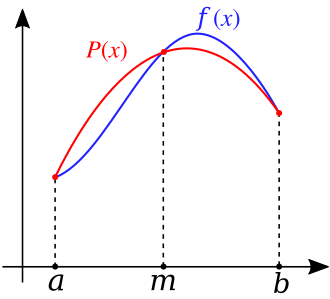
Z tego względu dla 2N + 1 punktów (czyli 2N przedziałów) funkcja będzie przybliżana przez N wielomianów:
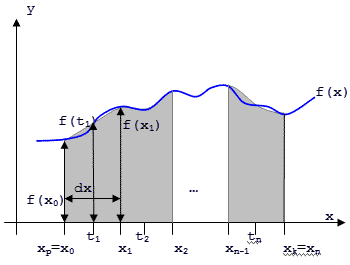
Całkę przybliżamy stosując następujący wzór:
Gdzie:
Ponieważ obliczenie całki wprost z tego wzoru wymagałoby (pomijając obliczanie xi) 3N - 1 dodawań, 2N mnożeń oraz N dzieleń, możemy dokonać przekształcenia, pozwalającego zredukować liczbę operacji arytmetycznych do 2N dodawań, 3 mnożeń i 1 dzielenia:
Implementacja w Pythonie
Dla przejrzystości pominiemy walidację argumentów i obsługę błędów.
Postać oryginalna
def simpson_integration_simple(my_func, a, b, n):
# Szerokość pojedynczego przedziału
delta_x = (b-a)/n
# x_i liczymy każdorazowo od nowa by uniknąć kumulowania
# się błędów numerycznych - kosztem dużej ilości mnożeń
total = 0
# pamiętamy że n = 2N
for i in range(0, n, 2):
x = a + delta_x * 2 * i
total += delta_x * (my_func(x) + 4 * my_func(x + delta_x) + my_func(x + 2 * delta_x) / 3
return total
# Wywołujemy naszą funkcję całkującą, przekazując wzór całkowanej funkcji jako lambdę
integral = simpson_integration_simple(lambda x: x**2, 0.0, 1.0, 100)
Postać przekształcona
def simpson_integration_modified(my_func, a, b, n):
# Szerokość pojedynczego przedziału
delta_x = (b-a)/n
total = my_func(a) + my_func(b)
subtotal_sum_1 = 0
subtotal_sum_2 = 0
# pierwsza suma, pamiętamy że n = 2N
for i in range(0, n, 2):
x = a + i * delta_x
subtotal_sum_1 += my_func(x)
# druga suma, pamiętamy że n = 2N
for i in range(1, n-1, 2):
x = a + i * delta_x
subtotal_sum_2 += my_func(x)
return delta_x * (total + 4 * subtotal_sum_1 + 2 * subtotal_sum_2) / 3
# Wywołujemy naszą funkcję całkującą, przekazując wzór całkowanej funkcji jako lambdę
integral = simpson_integration_modified(lambda x: x**2, 0.0, 1.0, 100)
Przykłady
Przykład 1: funkcja kwadratowa
TODO: przedstawić przykład krok po kroku z wynikami
Przykład 2: funkcja cosinus
TODO: przedstawić przykład krok po kroku z wynikami