Algorytm Knutha-Morrisa-Pratta
JumpSmerf
Algorytm KMP jest szybkim algorytmem wyszukiwania wzorca w tekście. Posiada pesymistyczną złożoność czasową liniową (O(n + m)).
Czym jest wyszukiwanie wzorca?
Wyszukiwanie wzorca w tekście polega na znalezieniu wszystkich wystąpień tekstu x zwanego wzorcem w tekście y. Długość tekstu będziemy oznaczać przez |x|. Przy czym |x| = m, |y| = n.
Aby wyznaczyć ilość wystąpień wzorca za pomocą algorytmu KMP trzeba najpierw poznać algorytm funkcji prefiksowej.
Mamy tablicę P[1..m], gdzie P[i] to jest długość najdłuższego właściwego prefikso-sufiksu jakiegoś słowa s[1..i] (mógłbym to pokazać na przykładzie któregoś ze słów wcześniej użytych, ale może to być jakiekolwiek słowo).
Formalnie zapisujemy: p[i] = max {0<=k<j: x[1..k] jest sufiksem x[1..j]}.
Co to właściwie jest?
Prefiks - początkowy fragment słowa.
Sufiks - końcowy fragment słowa.
Prefikso-sufiks - takie słowo, które występuje i na początku i na końcu
Graficznie:
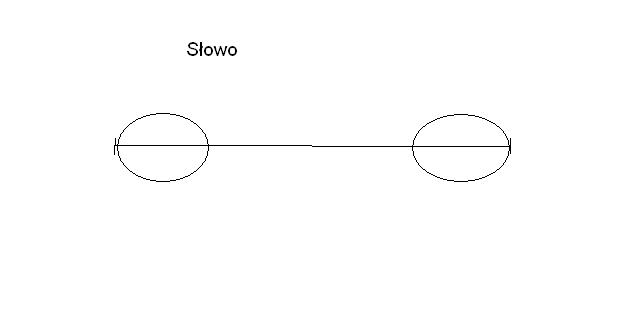
Mamy wyznaczyć długości najdłuższych właściwych prefikso-sufiksów poszczególnych prefiksów słowa.
Wystarczą do tego 2 lematy:
Lemat #1:
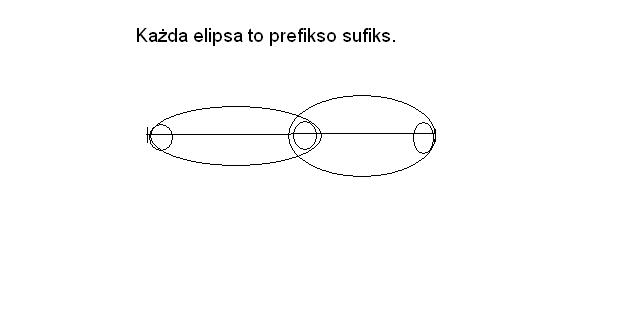
Prefikso-sufiks prefikso-sufiksa jest prefikso-sufiksem.
Oznacza to tyle, że jeżeli z jakiegoś słowa s wyznaczymy prefikso-sufiks, a następnie wydzielimy ten prefikso-sufiks i z niego wyznaczymy prefikso-sufiks, to ten wyznaczony właśnie prefikso-sufiks, prefikso-sufiksa jest prefikso-sufiksem s.
Dowód:
Skoro prefikso-sufiks występuje na początku i na końcu słowa s, to prefikso-sufiks prefikso-sufiksa s występuje w czterech miejscach. Dwa z tych miejsc to początek i koniec. Skoro prefikso-sufiks prefikso-sufiksa s występuje i na początku i na końcu to musi to być również prefikso-sufiks całego słowa s.
Przypadek 1:
Przypadek 2:

Zakładamy, że mamy policzone wartości funkcji prefiksowej dla danego słowa (to liczymy w lemacie #2).
Twierdzenie: Wszystkie prefikso-sufiksy słowa S[1..n] to: {n, p[n], P[P[n]],...}.
Ciąg jest ściśle malejący z granicą równą 0.
Gdybyśmy mieli to już wyznaczone, to przejście przez wszystkie prefikso-sufiksy jakiegoś słowa to iterowanie funkcji prefiksowej.
Lemat #2
Mamy wszystkie pozycje słowa s[1..i]. Patrzymy na pozycję i + 1. Jak mamy prefikso-sufiks tego całego słowa razem z i+1:
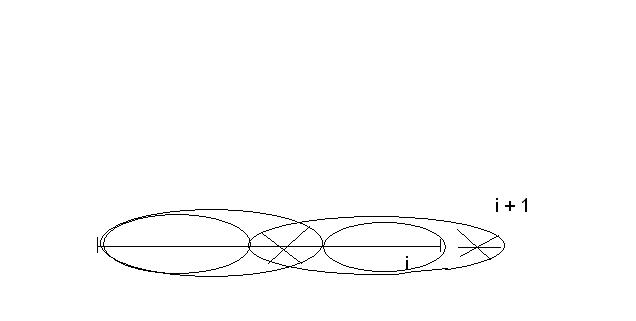
Wycinamy ostatnią literkę i mamy prefikso-sufiks słowa s[1..i].
W takim razie aby wyznaczyć P[i+1] musimy wziąć jakiś prefikso-sufiks słowa s[1..i], następnie taki w którym będzie odpowiednia literka, którą będziemy mogli przedłużyć. W ten sposób liczymy wartość prefikso-sufiksu dla P[i+1].
Innymi słowy aby policzyć P[i+1] wystarczy znaleźć taki prefikso-sufiks słowa s[1..i], który spełnia warunek s[t+1] = s[i+1] czyli taki, który można przedłużyć do prefikso-sufiksu s[1..i+1] (przy czym utożsamiamy prefikso-sufiksy słowa z ich długościami).
Przykład obliczania tablicy P można znaleźć na portalu [2].
Teraz właściwy algorytm:
- Pascal:
begin
P[0] = 0; P[1] := 0; t := 0; { najdłuższy prefikso-sufiks właściwy słowa jednoliterowego jest zawsze zero literowy }
for i := 2 to m do
begin { obliczamy wartość P[i] }
{ zawsze ma być właściwość t = P[i-1]}
while (t > 0) and (x[t+1] <> x[i]) do t := P[t]; { jeżeli natrafiłem na inną literkę to powracam do ostatniego prefikso-sufiksu}
if x[t+1] = x[i] then t := t + 1; p[i] := t { jeżeli to jednak ta sama literka to zwiększam t i zapisuję wynik }
end
end
Algorytm KMP wygodnie jest wykonywać na stringu indeksowanemu od 1, niestety tablice w C++ indeksowane są od 0. Można temu zaradzić przypisując na początku stringowi s jakiś dowolny znak w miejscu s[0]. Taka operacja będzie wymagała O(n) przesunięć, z jednej strony to dużo, z drugiej strony jest to mniej niż wykonuje algorytm KMP. Jeżeli ktoś jednak nie chce wykonywać takiej operacji, to może przerobić algorytm w taki sposób, aby działał dla tablic indeksowanych od 0.
- C++:
a) Z dodaniem jakiegoś znaku na początku:
{
n = s.size();
s = 'a' + s; // dla uproszczenia przypisujemy na początek jakiś dowolny znak
P[0] = 0; P[1] = 0; t = 0; // najdłuższy prefikso-sufiks właściwy słowa jednoliterowego jest zawsze zero literowy
for (int i = 2; i <= n; i++) { // obliczamy wartość P[i]; zawsze ma być właściwość t = P[i-1]
while (t > o && s[t+1] != s[i]) t = P[t]; // jeżeli natrafiłem na inną literkę to powracam do ostatniego prefikso-sufiksu
if (s[t+1] == s[i]) t++; // jeżeli to jednak ta sama literka to zwiększam t i zapisuję wynik
P[i] = t;
}
}
b) Bez dodania znaku na początku:
n = s.size();
P[0] = 0; P[1] = 0; t = 0;
for(int i = 1; i < n; i++) {
while (t > 0 && s[t] != s[i]) t = P[t-1];
if (s[t] == s[i]) t++;
P[i] = t;
}
Właściwy algorytm KMP:
Najczęściej algorytm KMP wyznacza się tak, że pisze się najpierw funkcję prefiksową, a później jeszcze jedną pętlę. Jest to niepotrzebne. Właściwie już mamy prawie cały kod.
Co wystarczy zrobić. Łączymy dwa wyrazy, w następujący sposób.
Mamy wzorzec x i tekst y.
Teraz wystarczy, że obliczamy tablicę prefikso-sufiksów dla słowa x#y, gdzie # jest specjalnym znakiem nie występującym w alfabecie, który chroni nas przed wyjściem poza wyjściem poza wzorzec. Dzięki temu jeżeli jeżeli P[i] będzie równe m, to w oznacza, że znaleźliśmy wzorzec, a w następnej iteracji wartość P[i+1] <= m (równa w przypadku jednoliterowego wzorca), ponieważ znak # ogranicza wzorzec.
Zmienia się bardzo niewiele, oto pseudokod:
- Pascal:
begin
s := x + '#' + y; { zakładam indeksowanie od 1 do n + m }
n = length(s);
p[0] := 0; P[1] := 0; t := 0;
for i := 2 to n do
begin
while (t > 0) and (s[t+1] <> s[i]) do t := P[t];
if s[t+1] = s[i] then t := t + 1;
P[i] := t;
if P[i] = m then w := w + 1 { w - ilość wystąpień wzorca; jeżeli długość sufiksa w tekście jest równa wzorcowi, to oznacza, że tu jest wzorzec }
end
end
- C++:
{
s = 'a' + x + '#' + y; // indeksowanie od 0, więc wygodnie znakowi zerowemu przypisać jakąś dowolną wartość
n = s.size() - 1;
P[0] = 0; P[1] = 0; t = 0;
for (int i = 2; i <= n; i++) {
while (t > 0 && s[t+1] != s[i]) t = P[t];
if (s[t+1] == s[i]) t++;
P[i] = t;
if (P[i] == m) w++; // w - ilość wystąpień wzorca; jeżeli długość sufiksa w tekście jest równa wzorcowi, to oznacza, że tu jest wzorzec
}
}
Złożoność:
Na pierwszy rzut oka wydaje się, że ten algorytm wcale nie działa w czasie liniowym. Jednak można udowodnić, że tak jest korzystając z analizy kosztu zamortyzowanego. W tym celu przypatrzmy się zmiennej t. Zmienna t zaczyna od zera i może zwiększyć swoją wartość co najwyżej n razy. Pętla while wykonuje się tylko wtedy gdy t jest większe zero, a jeżeli już ta pętla się wykonuje to t na pewno się zmniejszy. Skoro t może się zwiększyć co najwyżej n razy i zmniejsza się przy każdym wykonaniu pętli while, to instrukcja t = P[t] wykona się na pewno nie więcej niż n razy. W związku z tym ilość porównań w pętli while będzie mniejsza lub równa 2n. Zauważmy, że algorytm KMP jest w istocie tym samym, co algorytm funkcji prefiksowej, tyle, że wykonywany dla złączenia wzorca i tekstu, czyli złożoność algorytmu KMP to O(n+m).
Portale i literatura:
[1] http://was.zaa.mimuw.edu.pl/ (z tego w większości korzystałem przy funkcji prefiksowej, genialnie wytłumaczone)
[2] http://algorytm.org/ (odsyłam do przykładu)
[3] Algorytmy i struktury danych, L.Banachowski, K.Diks, W.Rytter (wziąłem z tego sam początek)
[4] Wprowadzenie do algorytmów, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein.
Polecam zadania:
- https://pl.spoj.pl/problems/KNUTH_PI/
- https://pl.spoj.pl/problems/KMP/
- http://main.edu.pl/pl/archive/oi/12/sza (trudniejsze zadanie, w razie problemów tu znajdziesz opis rozwiązania w odpowiedniej złożoności: http://oi.edu.pl/l/12oi_ksiazeczka/ ).
Jeżeli ten kod robi to co opisałeś to złożność jest taka samo jak w "klasycznym" KMP. Zgoda złożność twojego algorytmu to O(n). Jednak u ciebie "n" to długość słowa wzorzec#słowo. Natomiast w literaturze najczęściej podają O(n+m) gdzie "n" to długość słowa a "m" wzorca (lub na odwrót ;)). Jeżeli przyjmiemy takie oznaczenia u ciebie to dalej będzie to żłożność O(n+m). Dla pewności odwiedziłem pierwszy odnośnik żeby sprawdzić czy nie piszę głupot. Przynajmniej w notatkach piszą że chyba mam rację :). No chyba, że w tej pozycji książkowej pokazali coś ciekawego :p.