Raytracing w C# - część 1
msm
Część pierwsza z planowanych kilku artykułów na temat raytracingu.
Konwersja do składni Coyote robiona ręcznie, więc pewne błędy (np. złe formatowanie, brak ilustracji etc) mogłem przeoczyć.
Jeśli to możliwe, polecam z tekstem zapoznawać się z oryginalnego dokumentu: ray.1.pdf
Raytracing: krok po kroku
cz. 1 - pierwsze kroki
I. Co/Dlaczego?
W tym artykule postaram się opisać absolutne podstawy raytracingu - w sposób maksymalnie przystępny dla kogoś kto nie miał ze ‘śledzeniem promieni’ dotychczas nic wspólnego.
O raytracingu napisano już niejeden artykuł - znalezienie dowolnego z nich w olbrzymich zasobach internetu nie powinno (szczególnie dla kogoś kto uważa się za informatyka) stanowić żadnego problemu - problemem jest to że z reguły autorzy rzucają czytelnika od razu na naprawdę głęboką wodę, przez co wiele osób odbija się szybko od tematu.
Moim celem jest krótkie opisanie sposobu działania i poprowadzenia krok po kroku przez implementację. W artykułach będzie podany zawsze kompletny kod, więc można 'napisać' raytracer nie rozumiejąc zupełnie jego działania, nie czytając opisów a jedynie kopiując gotowy kod - bardzo nie polecam takiego podejścia.
Niestety, nie należy oczekiwać wspaniałych efektów wizualnych po użyciu kodu stworzonego w tym artykule. Przedstawiony jest tu dosłownie szkielet prawdziwego raytracera, a to co pozwala na generowanie oszałamiających obrazów (czyli zabawy ze światłem, cieniem i odbiciem) może spokojnie zostać dodane - w następnych częściach.
Ostatnia uwaga - przez cały artykuł posługuję się pojęciem 'promienia' mając na myśli półprostą. Po prostu w kontekście raytracingu to słowo jest bardziej... odpowiednie.
II. Wstęp teoretyczny
Raytracing różni się bardzo od podejścia zwykle stosowanego w tworzeniu grafiki 3D. Nie ma tu trójkątów, a przynajmniej nie są one podstawowym składnikiem sceny. Więc na czym koncentrujemy się najbardziej? Jak sama nazwa wskazuje - na promieniach.
“Zwykła” grafika trójwymiarowa którą widzimy na przykład w grach komputerowych jest dość abstrakcyjna i, wbrew pozorom, prymitywna. Nie ma też nic wspólnego z właściwościami fizycznymi świata jaki oglądamy codziennie. Z punktu widzenia komputera, mówiąc prostymi słowami, pewna ilość punktów jest rzutowana do dwóch wymiarów. Punkty te są następnie łączone w trójkąty, które z kolei wypełniane są odpowiednimi kolorami.
Raytracing podchodzi do problemu udawania 3D zupełnie inaczej. Renderowanie obrazu polega na wypuszczeniu promieni z kamery i obserwowaniu tego co się z nim dzieje na ich drodze.
III. Pierwsze kroki
Do napisania raytracera konieczny będzie odpowiedni zestaw klas pomocniczych. Pierwszym narzędziem właściwie niezbędnym do tego żeby przejść dalej jest wszechobecny w prawie każdym programie związanym z grafiką/fizyką wektor.
Myślę że każdy zabierający się za raytracing czy ogólnie, grafikę trójwymiarową, wie czym jest wektor, ale dla porządku wypada o tym napisać. Wektor można przedstawić jako trzy wartości zmiennoprzecinkowe
reprezentujące odpowiednio współrzędne X, Y i Z. Operacje jakich potrzebujemy od wektora to przede wszystkim dodawanie i odejmowanie drugiego wektora, mnożenie przez skalar oraz dot product.
IV. Typ reprezentujący wektor:
Pisanie kodu wektora rozpoczynamy od stworzenia reprezentującej go struktury. Można od razu dorzucić tam deklarację odpowiednich zmiennych oraz wygodny konstruktor.
struct Vector3
{
public double X { get; set; }
public double Y { get; set; }
public double Z { get; set; }
public Vector3(double x, double y, double z)
: this()
{
this.X = x;
this.Y = y;
this.Z = z;
}
}
Jeśli piszesz w C# i zastanawia Cię dlaczego została użyta struktura a nie klasa, oto wyjaśnienie:
Po pierwsze - dla wydajności. Na wektorze będziemy wykonywać dziesiątki milionów operacji podczas renderowania bardziej skomplikowanych scen. Struktura jest odpowiedniejsza do tego typu zastosowań.
Po drugie - usuwa to pewne problemy związane z przekazywaniem przez referencje - chcemy żeby był typem jak najprostszym, nie pożądamy współdzielenia referencji do niego.
Po trzecie - właśnie dla takich sytuacji struktury powstały - szkoda byłoby żeby się marnowały.
Dodawanie i odejmowanie wektorów to po prostu dodawanie i odejmowanie odpowiednich współrzędnych:
public static Vector3 operator +(Vector3 vec1, Vector3 vec2)
{
return new Vector3(vec1.X + vec2.X, vec1.Y + vec2.Y, vec1.Z + vec2.Z);
}
public static Vector3 operator -(Vector3 vec1, Vector3 vec2)
{
return new Vector3(vec1.X - vec2.X, vec1.Y - vec2.Y, vec1.Z - vec2.Z);
}
Mnożenie i dzielenie przez skalar jest równie oczywiste:
public static Vector3 operator *(Vector3 vec, double val)
{
return new Vector3(vec.X * val, vec.Y * val, vec.Z * val);
}
public static Vector3 operator /(Vector3 vec, double val)
{
return new Vector3(vec.X / val, vec.Y / val, vec.Z / val);
}
Trochę mniej intuicyjną operacją jest Dot Product, inaczej zwany iloczynem skalarnym wektorów. Mimo strasznej nazwy, jest to po prostu suma iloczynów częściowych - czyli, bardziej 'informatycznie', x1x2 + y1y2 + z1*z2 dla wektorów trójwymiarowych:
public double Dot(Vector3 vec)
{
return (this.X * vec.X + this.Y * vec.Y + this.Z * vec.Z);
}
Poza iloczynem skalarnym istnieje jeszcze pojęcie iloczyna wektorowego - nie trzeba rozumieć tego co dzieje się w tej funkcji, najważniejsze to zapamiętać że zwraca on wektor prostopadły do obydwóch mnożonych wektorów:
public static Vector3 Cross(Vector3 vec1, Vector3 vec2)
{
return new Vector3(vec1.Y * vec2.Z - vec1.Z * vec2.Y,
vec1.Z * vec2.X - vec1.X * vec2.Z,
vec1.X * vec2.Y - vec1.Y * vec2.X);
}
Przydadzą się jeszcze dwie metody obliczające odpowiednio długość i kwadrat długości wektora:
public double Length
{ get { return Math.Sqrt(X * X + Y * Y + Z * Z); } }
public double LengthSq
{ get { return X * X + Y * Y + Z * Z; } }
i ostatecznie, normalizacja wektora (zmiana długości wektora do 1, przy zachowaniu proporcji między bokami):
public Vector3 Normalised
{ get { return this / this.Length; } }
Dodatkowo czasami wygodne będzie posługiwanie się wektorem dwuwymiarowym - ale ponieważ praktycznie wszystkie obliczenia wykonujemy w trójwymiarze, nie ma potrzeby pisać dla niego operacji arytmetycznych (chociaż oczywiście można):
struct Vector2
{
public double X { get; set; }
public double Y { get; set; }
public Vector2(double x, double y)
: this()
{
this.X = x;
this.Y = y;
}
}
Gotowe.
V. Typ reprezentujący promień:
Promień można zdefiniować jako zbiór punktów spełniających równianie
p = o + t*d
Gdzie o to początek promienia a d to kierunek. Zmienna t przyjmuje wartości od 0 do nieskończoności.
Nasza reprezentacja promienia, inaczej niż wektora, będzie tylko prostym pojemnikiem na dane, bez własnej logiki.
Najwygodniej dla naszych celów jest przechowywać informacje o początku (origin) i kierunku (direction). Odpowiada temu taka prosta struktura:
struct Ray
{
public const double Epsilon = 0.00001;
public const double Huge = double.MaxValue;
public Ray(Vector3 origin, Vector3 direction)
: this()
{
this.Origin = origin;
this.Direction = direction.Normalised;
}
public Vector3 Origin { get; set; }
public Vector3 Direction { get; set; }
}
Kierunek promienia musi być znormalizowany, stąd uzycie właściwości Normalised w konstruktorze.
Wyjaśnienia wymagają też stałe Epsilon i Huge - oznaczają odpowiednio długość pewnego dowolnego bardzo krótkiego promienia i dowolnego bardzo długiego promienia (można je spokojnie powiększyć o pare zer).
Epsilon służy do porównywania liczb zmiennoprzecinkowych - nie można porównywać ich dokładnych wartości z powodu drobnych błędów arytmetycznych przy obliczeniach na liczbach zmiennoprzecinkowych. Zamiast tego porównywane są z przedziałem tolerancji równym epsilon właśnie.
Huge za to powinien mieć zagwarantowaną wartość większą niż najdalszy obiekt na scenie. Służy do oznaczania że promień nie trafił w żaden obiekt (czyli poleciał w nieskończoność = Huge).
VI. Obiekty w świecie:
Po napisaniu niezbędnych klas pomocniczych, możemy zacząć zajmować się pisaniem kodu faktycznie związanego z projektem.
Pisanie raytracera zaczniemy od stworzenia typów reprezentujących proste bryły/figury geometryczne - 'cegiełki' z których będziemy budować świat przedstawiony na scenie. Skorzystamy w tym celu z możliwości programowania obiektowego.
Jak powinna 'działać' taka figura (czyli w jaki sposób miałaby być używana)? Tak jak wspomniałem wcześniej, raytracing polega na śledzeniu promieni, analizowaniu tego co się dzieje z nimi po drodze i ustalaniu na tej podstawie odpowiedniego koloru piksela. W pseudokodzie wygląda to mniej-więcej tak:
function Raytrace(bitmap, scene):
for each(pixel in bitmap):
ray = CreateRayFromPixel(pixel) ; stwórz promień w kierunku piksela na obrazie
bitmap[pixel] = TraceRay(scene, ray) ; sprawdź jaki kolor ma obiekt na który trafił
CreateRayFromPixel ustala kierunek promienia na podstawie koordynatów piksela na obrazku. To nic innego niż kamera - od tej funkcji zależy to skąd patrzymy na scenę, w jakim kierunku patrzymy, pole widzenia, etc. Napisanie takiej funkcji jest dość proste, ale pozostaje jeszcze jedna rzecz do wyjaśnienia, rzecz właściwie najważniejsza - w jaki sposób śledzić promień (TraceRay)?
Nie jest to tak skomplikowane jak się wydaje. W pseudokodzie odpowiada za to funkcja TraceRay, którą działa w sposób podobny do takiego:
function TraceRay(scene, ray):
lastHitDistance = Infinity ; odl. do najbliższego obiektu
hitObject = null ; trafiony obiekt (najbliższy kamerze)
for each(currObject in scene):
hitInfo = object.HitTest(ray) ; sprawdź czy promień trafia obiekt
if (hitInfo.Hit && lastHitDistance > hitInfo.Distance): ; jeśli jest to najbliższe trafienie
hitObject = currObject ; nowy trafiony obiekt
lastHitDistance = hitInfo.Distance ; nowa najmniejsza odległość
if (hitObject == null):
return backgroundColor ; jeśli w nic nie trafiliśmy zwróć kolor tła
else
return hitObject.Color ; zwróć kolor trafionego obiektu
Jak widać nie ma tu żadnej magii - ale to jeszcze nie wszystko. W piątej linijce kryje się niepozorne wyrażenie object.HitTest(ray) - odpowiada ono za sprawdzenie czy promień przecina obiekt i, jeśli tak, wypełnienie odpowidnich pól struktury hitInfo (musi zasygnalizować czy trafienie nastąpiło i jeśli tak, w jakiej odległości nastąpiło. Faktyczny kod w C# będzie się obchodził bez tej struktury a zamiast tego będzie użyte przekazywanie parametrów przez referencję, ale zasada działania wszędzie jest taka sama).
To jest właśnie to czego potrzebujemy od obiektu żeby móc go narysować - metoda sprawdzająca przecięcie z promieniem - tylko tyle. Stwarza to bardzo duże możliwości definiowania obiektów i nie ogranicza nas do prymitywnych trójkątów - można używać wszystkich kształtów które można zdefiniować za pomocą funkcji - kulę, powierzchnię, trójkąt, ale nic (oprócz wyobraźni) nie stoi na przeszkodzie żeby renderować na przykład zbiór mandelbrota.
Skoro odkryliśmy grupę obiektów mających wspólną cechę - można sprawdzić przecięcie promienia z nimi - wypada stworzyć odpowiednią klasę abstrakcyjną która sformalizuje to powiązanie. Nazwiemy ją GeometricObject:
abstract class GeometricObject
{
public Color Color { get; set; }
public abstract bool HitTest(Ray ray, ref double distance);
}
Tak jak ostrzegałem, jest tutaj drobna różnica w porównaniu do pseudokodu: HitTest zamiast zwracać strukturę wykorzystuje referencję do przekazania odległości od punktu trafienia. Dodatkowo obiekt musi przechowywać swój kolor (w przyszłości kolor zostanie zamieniony na materiał).
VII. Sfera - teoria:
Mimo obietnic o unikaniu teorii i koncentrowaniu się na praktyce, raytracing bardzo silnie wiąże się z matematyką i fizyką. Możliwe jest pominięcie tej sekcji i kontynuowanie czytania od części praktycznej, ale zalecane jest chociaż pobieżne przeglądnięcie w celu zrozumienia co z czego wynika, z pewnością przyda się to przy próbach samodzielnego rozszerzenia programu.
Pierwszym obiektem który będziemy modelować jest sfera. Z matematycznego punktu widzenia, sfera to zbiór punktów jednakowo odległych (o promień) od pewnego punktu (środka).
Żeby móc go narysować, potrzebujemy sposobu na znalezienie punktu przecięcia promienia ze sferą. Równanie promienia było już podane:
p = o + t*d
Równanie sfery można zapisać w następujący sposób:
(p-c)•(p-c)-r^2
Można teraz ułożyć układ równań i rozwiązać go dla zmiennej t:
(p-c)•(p-c)-r^2
p = o + t*d
Po podstawieniu otrzymujemy:
(o+t*d-c)•(o+t*d-c)-r^2 = 0
Rozwijając dot product:
(d•d)t^2 + [2(o-c)•d]t+(o-c)•(o-c)-r^2 = 0
Jest to równanie kwadratowe w postaci
a*t^2 + b*t + c = 0
gdzie
a = d•d
b = 2(o-c)•d
c=(o-c)•(o-c)-r^2
Rozwiązania równania kwadratowego można otrzymać w prosty sposób:
Δ=b*b-4*a*c
t1 = (-b+sqrt(Δ))/(2*a)
t2 = (-b-sqrt(Δ))/(2*a)
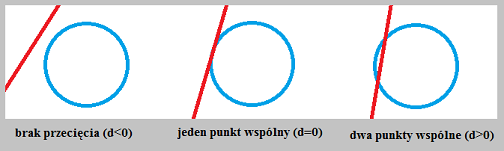
W zależności od wartości równanie może mieć 2 ( Δ>0 ), 1 ( Δ=0 ) lub 0 ( Δ<0 ) rozwiązań, co ma odbicie w fakcie że promień może przeciąć sferę w 0 (brak trafienia), 1 lub 2 miejscach (w tym wypadku interesuje nas bliższe przecięcie).
Pokazuje to ilustracja przygotowana przez profesjonalnego grafika:
VIII. Sfera - praktyka:
Czas równania z poprzedniego akapitu przerobić na kod. Zaczynamy oczywiście od stworzenia klasy Sphere dziedziczącej po GeometricObject:
class Sphere : GeometricObject
{
Vector3 center;
float radius;
public Sphere(Vector3 center, float radius, Color color)
{
this.center = center;
this.radius = radius;
base.Color = color;
}
public override bool HitTest(Ray ray, ref double distance)
{
throw new System.NotImplementedException();
}
}
Teraz trzeba uzupełnić automatycznie wygenerowany kod tym właściwym. Gotowiec, bezpośrednia implementacja wyprowadzonych przed chwilą wzorów:
public override bool HitTest(Ray ray, ref double minDistance)
{
double t;
Vector3 distance = ray.Origin - center;
double a = ray.Direction.LengthSq;
double b = (distance * 2).Dot(ray.Direction);
double c = distance.LengthSq - radius * radius;
double disc = b * b - 4 * a * c;
if (disc < 0) { return false; }
double discSq = Math.Sqrt(disc);
double denom = 2 * a;
t = (-b - discSq) / denom;
if (t < Ray.Epsilon)
{ t = (-b + discSq) / denom; }
if (t < Ray.Epsilon)
{ return false; }
minDistance = t;
return true;
}
IX. Kamera:
Ostatnim problemem który dzieli nas od zakończenia projektu jest kamera. Nasza kamera będzie działała w następujący sposób: przyjmuje dwuwymiarowy punkt (Vector2) z zakresu [-1, -1] (lewy, górny róg widocznego obrazu) do [1, 1] (prawy, dolny róg widocznego obrazu) i zwraca odpowiedni promień. Zaczniemy oczywiście od odpowiedniej klasy abstrakcyjnej (a właścieie, w tym przypadku, odpowiedniego interfejsu):
interface ICamera
{
Ray GetRayTo(Vector2 relativeLocation);
}
Być może na początku wydaje się to niepotrzebną komplikacją - taki ogólny interfejs daje nam jednak bardzo duże możliwości w tworzeniu różnych wariacji na temat kamery - od realistycznej kamery perspektywicznej, przez ortogonalną, aż do ciekawych efektów jak np. kamera fish-eye czy sferyczna.
Najprostszą kamerą jest kamera ortogonalna - wszystkie promienie wychodzące mają taki sam kierunek. Taką właśnie na początek zaimplementujemy.
Patrzenie na świat z dowolnym kątem i obrotem wymaga wykonania kilku prostych i szybkich w działaniu, ale niekoniecznie łatwych do zrozumienia operacji na wektorach - dlatego chwilowo pozwolimy sobie tylko na obrót wokół osi Y.
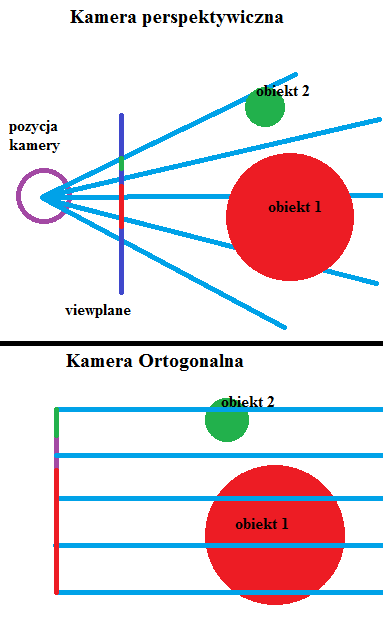
Kamera ortogonalna ma wiele zastosowań - głównie naukowych do prezentacji symulacji fizycznych i chemicznych oraz przy modelowaniu obiektów 3d. Jej zaletą jest brak zniekształceń perspektywy - rozmiar obiektów na ekranie niezależnie od odległości do oka, co umożliwia dokładną analizę ich wielkości i proporcji. Niestety jest to też jej największa wada - działa zupełnie inaczej niż oko ludzkie, przez co jest kompletnie nieprzekonująca przy renderowaniu. Dlatego też już niedługo zmienimy ją na inną, bardziej naturalną kamerę perspektywiczną.
Dla ciekawych, kolejny profesjonalny rysunek:
Na początek jak zwykle szablon klasy:
class Orthogonal : ICamera
{
public Vector3 EyePosition { get; set; }
public double Angle { get; set; }
public Vector2 CameraSize { get; set; }
public Orthogonal(Vector3 eye, double angle, Vector2 size)
{
this.EyePosition = eye;
this.Angle = angle;
this.CameraSize = size;
}
public Ray GetRayTo(Vector2 pictureLocation)
{
throw new System.NotImplementedException();
}
}
Teraz rozwiniemy metodę GetRayTo:
public Ray GetRayTo(Vector2 pictureLocation)
{
// Kierunek w którym skierowane są wszystkie promienie
// wychodzące z kamery.
// Otrzymany prostymi funkcjami trygonometrycznymi.
Vector3 direction = new Vector3(
Math.Sin(Angle),
0,
Math.Cos(Angle));
// Kierunek promienia zawsze musi być znormalizowany.
direction = direction.Normalised;
// Jak bardzo początek promienia jest oddalony od
// położenia kamery
Vector2 offsetFromCenter = new Vector2(
pictureLocation.X * CameraSize.X,
pictureLocation.Y * CameraSize.Y);
// Obliczenie finalnego położenia kamery,
// rówież proste funkcje trygonometryczne.
Vector3 position = new Vector3(
EyePosition.X + offsetFromCenter.X * Math.Cos(Angle),
EyePosition.Y + offsetFromCenter.Y,
EyePosition.Z + offsetFromCenter.X * Math.Sin(Angle));
return new Ray(
position,
direction);
}
Nasza kamera ortogonalna jest bardzo prymitywna, nie umożliwia na przykład patrzenia w górę lub 'robienia beczek'. Bardziej przyjrzymy się tworzeniu kamer w następnych częściach.
X. Raytracing:
Objętość artykułu zwiększa się nieubłaganie i obiecana minimalistyczność jest coraz dalej. Czas wreszcie połączyć wszystko razem i stworzyć działający, chociaż prosty, raytracer. Warto wrócić trochę do tyłu i przeanalizować pseudokody podane w akapicie VI.
Kod który napiszemy nie będzie dokładnie tak samo wyglądał jak pseudokod - głównie dlatego że nasz program jest pisany obiektowo i zgodnie z zasadami S.O.L.I.D.
Przede wszystkim wprowadzimy pomocniczą klasę HitInfo - prawda, w tym momencie jest ona właściwie niepotrzebna (można ją zastąpić za pomocą Color?.), ale po pierwsze - informacja o trafieniu znacznie bardziej niż nullable color oddaje to co zwraca śledzenie promienia i po drugie - HitInfo mocno się rozrośnie i zyska na znaczeniu podczas obsługi oświetlenia i cieniowania. Tak czy inaczej, jest to tylko pojemnik z dwoma prostymi polami:
class HitInfo
{
public bool HitObject { get; set; }
public Color Color { get; set; }
}
Klasa World reprezentuje zbiór wszystkich obiektów na scenie. Udostępnia też metodę TraceRay która zwraca HitInfo dla danego w parametrze Ray-a (była ona omówiona wcześniej w pseudokodzie).
class World
{
List<GeometricObject> objects;
public World(Color background)
{
this.BackgroundColor = background;
this.objects = new List<GeometricObject>();
}
public void Add(GeometricObject obj)
{
objects.Add(obj);
}
public HitInfo TraceRay(Ray ray)
{
HitInfo result = new HitInfo();
double minimalDistance = Ray.Huge; // najbliższe trafienie
double hitDistance = 0; // zmienna pomocnicza, ostatnia odległość
foreach (var obj in objects)
{
if (obj.HitTest(ray, ref hitDistance) &&
hitDistance < minimalDistance) // jeśli najbliższe trafienie
{
minimalDistance = hitDistance; // nowa najmniejsza odległość
result.HitObject = true; // trafiono obiekt
result.Color = obj.Color; // zapisz kolor trafionego obiektu
}
}
return result;
}
public Color BackgroundColor { get; private set; }
}
Właściwość BackgroundColor to tło - na taki kolor ustawiamy piksel jeśli na nic nie trafimy.
Metoda TraceRay jest opisana wcześniej przez pseudokod - szukamy najbliższego obiektu na drodze trafienia.
No i ostatecznie - klasa która śledzi promienie dla każdego piksela i tworzy obraz wynikowy :
class Raytracer
{
public Bitmap Raytrace(World world, ICamera camera, Size imageSize)
{
Bitmap bmp = new Bitmap(imageSize.Width, imageSize.Height);
for(int x = 0; x < imageSize.Width; x++)
for (int y = 0; y < imageSize.Height; y++)
{
// przeskalowanie x i y do zakresu [-1; 1]
Vector2 pictureCoordinates = new Vector2(
(x / (double)imageSize.Width) * 2 - 1,
(y / (double)imageSize.Height) * 2 - 1);
// wysłanie promienia i sprawdzenie w co właściwie trafił
Ray ray = camera.GetRayTo(pictureCoordinates);
HitInfo info = world.TraceRay(ray);
// ustawienie odpowiedniego koloru w obrazie wynikowym
Color color;
if (info.HitObject) { color = info.Color; }
else { color = world.BackgroundColor; }
bmp.SetPixel(x, y, color);
}
return bmp;
}
}
Gotowe - w ten sposób skończyliśmy projekt raytracera. Aby nacieszyć oczy efektem działania trzeba jeszcze stworzyć jakąś scenę - moja propozycja to najbardziej chyba kultowa scena czyli trzy różnokolorowe kule.
class Program
{
static void Main(string[] args)
{
// Stworzenie świata (kolor tła = łagodny niebieski)
World world = new World(Color.PowderBlue);
// Trzy różnokolorowe kule (patrz obrazek)
world.Add(new Sphere(new Vector3(-2.5, 0, 0), 2, Color.Red));
world.Add(new Sphere(new Vector3(2.5, 0, 0), 2, Color.Green));
world.Add(new Sphere(new Vector3(0, 0, 2.5), 2, Color.Blue));
// Kamera w punkcie (0, 0, -5), skierowana w kierunku kul. Obszar obejmowany kamerą to 5x5.
ICamera camera = new Orthogonal(new Vector3(0, 0, -5), 0, new Vector2(5, 5));
Raytracer tracer = new Raytracer();
// Raytracing!
Bitmap image = tracer.Raytrace(world, camera, new Size(256, 256));
// Zapisanie obrazka w jakimś miłym miejscu na dysku.
image.Save("raytraced.png");
}
}
I co jest wynikiem tych wszystkich starań? Cóż...

Zgadza się - jeszcze wiele brakuje zanim efekty pracu naszego programu będą powodowały opad szczęki u znajomych, ale... pierwszy krok został uczyniony.
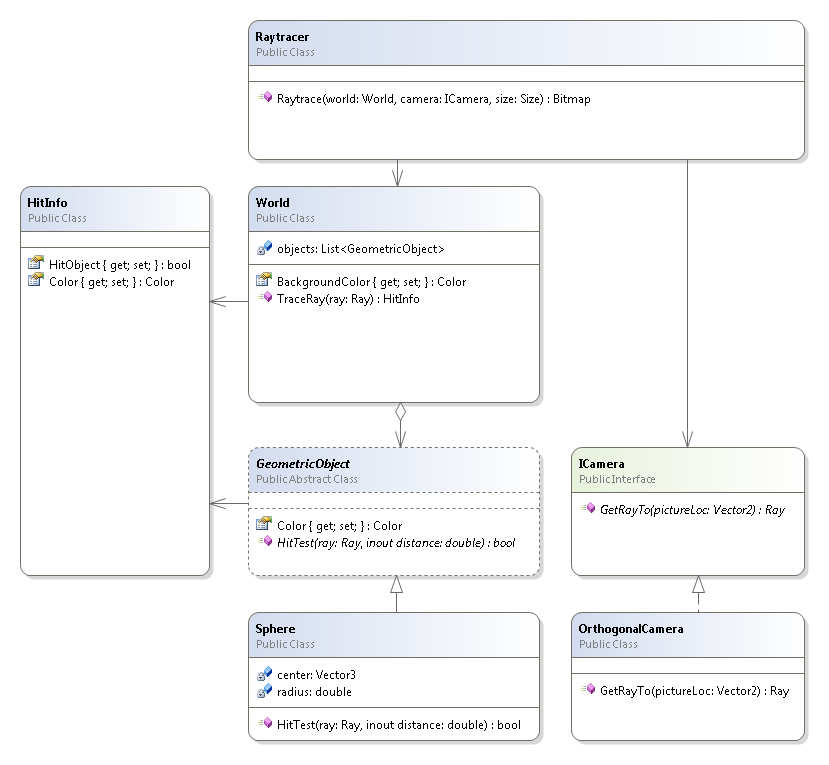
Dodany diagram klas biorących udział w renderowaniu: