Sito Eratostenesa
Thomashek
Sito Eratostenesa jest algorytmem służącym do wyznaczenia wszystkich liczb pierwszych z zakresu od 2 do danego n. Działanie algorytmu polega na wykreślaniu z danego zbioru (2, 3, 4, ..., n) wszystkich wielokrotności kolejnych liczb (większych od nich), które nie zostały do tej pory wykreślone, przy czym wystarczy wziąć pod uwagę tylko liczby z zakresu od 2 do wartości całkowitej z ?n. Wszystkie liczby, które pozostaną niewykreślone, są liczbami pierwszymi.
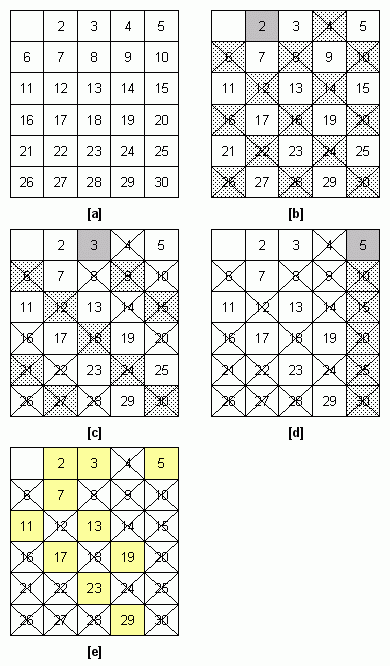
Rys. 1. Działanie algorytmu na przykładowym zbiorze liczb. Wykreślamy wielokrotności kolejnych, niewykreślonych liczb (2, 3, 5) - analizujemy liczby od 2 do 5 (jest to wartość całkowitą ?30). Po zakończeniu działania algorytmu otrzymujemy zbiór liczb pierwszych z zakresu od 2 do 30 (liczby na żółtym tle).
Zastosowanie
Skutkiem działania algorytmu jest zbiór kolejnych liczb pierwszych z danego zakresu. Zbiór ten jest przydatny przy rozkładzie liczb na czynniki pierwsze, co z kolei jest wykorzystywane przy wyznaczaniu ilości dzielników liczby.
Implementacja
Najprościej rozwiązać problem, deklarując tablicę elementów z indeksami do liczby n i wykonać operację sprawdzania, które elementy tablicy nie zostały jeszcze wykreślone, za pomocą głównej pętli sprawdzającej oraz wykreślać wielokrotności owych liczb za pomocą kolejnej pętli. Poniżej implementacja zapisana za pomocą pseudokodu:
przypisz wszystkim elementom tablicy tablica początkową wartość logiczną TRUE
for od i = 2 do i = wartość całkowita z ?n do
{
if tablica[i] == TRUE then
{
j = 2 * i //najmniejsza wielokrotność większa od danej liczby
while j <= n do
{
tablica[j] = FALSE //wykreślenie liczby
j = j + i //przejdź do kolejnej wielokrotności
}
}
}
barszo bym prosił o napiaanie algorytmu do LIPS-a
Opis
Mnie się podoba
Zastosowania
Jest ich dramatycznie więcej. ;-)
Implementacja
Wszystko ;-) no może prawie wszystko da się usprawnić.
Oto algorytm troszkę lżejszy, +/- dwa razy szybszy.
for i= 0..n-1
tablica[i]=TRUE
for i= 4..n-1 STEP 2
tablica[i]=FALSE // bardzo istotne
for i= 2..sqrt(n)
if tablica[i]
j= ii
while j < n
tablica[j]= FALSE
j+= i2
Nie.. to nie gotowiec - to artykuł!
Każdy programista sam sobie przepisze pseudokod do języka, którego używa.
Podoba mi sie sposob opisywania przez Ciebie algorytmow, rysunek opis, implementacja. Oby tak dalej! Mi tylko oprocz implementacji w pseudokodzie brakuje tylko przykladu "gotowca" w jakims istniejacym.
Plus za implementację w pseudokodzie a nie jakimś istniejącym.